命題p:滿足關于x的不等式2x2-9x+a<0(解集非空)的每一個x的值至少滿足不等式x2-4x+3<0和x2-6x+8<0中的一個;命題q:函數y=lg(ax2-x+a)的定義域為R.
(1)求命題p成立時a的取值范圍;
(2))如果“p∧q”為假,“p∨q”為真,求實數a的取值范圍.
【答案】
分析:(1)根據已知可得不等式2x
2-9x+a<0的解集為A與不等式x
2-4x+3<0解集為B和不等式x
2-6x+8<0解集為C滿足,A⊆B∪C,結合二次函數的圖象和性質及集合之間包含關系的定義,可構造不等式組,進而求出命題p成立時a的取值范圍;
(2)根據“p∧q”為假,“p∨q”為真,結合復合命題真值表可得p,q為一真一假,分類討論后可得實數a的取值范圍.
解答:解:(1)設不等式2x
2-9x+a<0的解集為A(非空)
不等式x
2-4x+3<0解集為B=(1,3)
不等式x
2-6x+8<0解集為C=(2,4)
則B∪C=(1,4)
∵關于x的不等式2x
2-9x+a<0(解集非空)的每一個x的值至少滿足不等式x
2-4x+3<0和x
2-6x+8<0中的一個
∴A⊆B∪C
∴
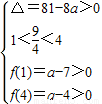
解得7<a<
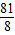
即命題p成立時a的取值范圍為(7,
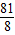
)
(2)若命題q:函數y=lg(ax
2-x+a)的定義域為R為真,則
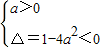
,解得a>

又∵“p∧q”為假,“p∨q”為真,
∴p,q為一真一假
當p真q假時,
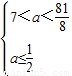
,此時無滿足條件的a值;
當p假q真時,
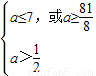
,解得

<a≤7,或a≥
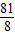
綜上,實數a的取值范圍為(

,7]∪[
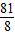
,+∞)
點評:本題以復合函數的真假為載體考查了不等式的解法及集合關系的判斷,其中解答二次不等式是解答本題的關鍵.

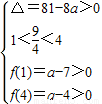
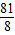
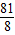 )
)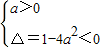 ,解得a>
,解得a>
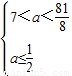 ,此時無滿足條件的a值;
,此時無滿足條件的a值;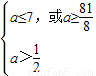 ,解得
,解得 <a≤7,或a≥
<a≤7,或a≥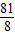
 ,7]∪[
,7]∪[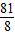 ,+∞)
,+∞)

 習題精選系列答案
習題精選系列答案