
已知函數 ,函數
,函數 .
.
⑴當 時,函數
時,函數 的圖象與函數
的圖象與函數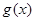 的圖象有公共點,求實數
的圖象有公共點,求實數 的最大值;
的最大值;
⑵當 時,試判斷函數
時,試判斷函數 的圖象與函數
的圖象與函數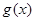 的圖象的公共點的個數;
的圖象的公共點的個數;
⑶函數 的圖象能否恒在函數
的圖象能否恒在函數 的上方?若能,求出
的上方?若能,求出 的取值范圍;若不能,請說明理由.
的取值范圍;若不能,請說明理由.
(1) 的最大值為
的最大值為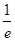 ,(2)
,(2)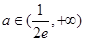 時,無公共點,
時,無公共點,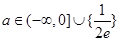 時,有一個公共點,
時,有一個公共點,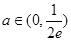 時,有兩個公共點;(3)當
時,有兩個公共點;(3)當 或
或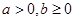 時函數
時函數 的圖象恒在函數
的圖象恒在函數 的圖象的上方.
的圖象的上方.
解析試題分析:(1)當 時,由圖形可知一次函數
時,由圖形可知一次函數 與對數函數
與對數函數 相切時,
相切時, 取最大值,可以用導數的幾何意義完成;(2)要研究兩函數的公共點個數,由函數
取最大值,可以用導數的幾何意義完成;(2)要研究兩函數的公共點個數,由函數 的定義域可知只需考慮
的定義域可知只需考慮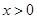 情況,當
情況,當 時,令
時,令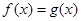 得
得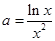 ,則原命題等價于研究直線
,則原命題等價于研究直線 與函數
與函數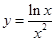 的圖象的公共點的個數,因此利用導數研究函數
的圖象的公共點的個數,因此利用導數研究函數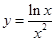 圖象變化情況,易得結論;(3)把問題轉化為:
圖象變化情況,易得結論;(3)把問題轉化為: 在
在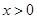 時恒成立問題,要注意對
時恒成立問題,要注意對 取值情況的討論.
取值情況的討論.
試題解析:⑴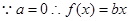 ,由一次函數與對數函數圖象可知兩圖象相切時
,由一次函數與對數函數圖象可知兩圖象相切時 取最大值,設切點橫坐標為
取最大值,設切點橫坐標為 ,
,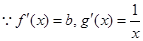 ,
,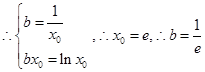 , 即實數
, 即實數 的最大值為
的最大值為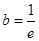 ,⑵
,⑵ ,即原題等價于直線
,即原題等價于直線 與函數
與函數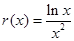 的圖象的公共點的個數,
的圖象的公共點的個數,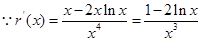 ,
,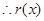 在
在 遞增且
遞增且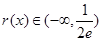 ,
,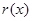 在
在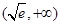 遞減且
遞減且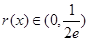 ,
,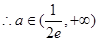 時,無公共點,
時,無公共點,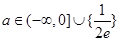 時,有一個公共點,
時,有一個公共點,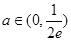 時,有兩個公共點;⑶函數
時,有兩個公共點;⑶函數 的圖象恒在函數
的圖象恒在函數 的上方;即
的上方;即 在
在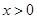 時恒成立,①
時恒成立,①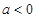 時
時 圖象開口向下,即
圖象開口向下,即 在
在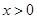 時不可能恒成立,②
時不可能恒成立,②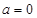 時
時 ,由⑴可得
,由⑴可得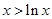 ,
, 時
時 恒成立,
恒成立,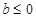 時
時 不成立,③
不成立,③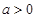 時,若
時,若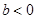 則
則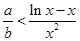 ,由⑵可得
,由⑵可得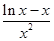 無最小值,故
無最小值,故 不可能恒成立,若
不可能恒成立,若 則
則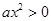 ,故
,故 恒成立,若
恒成立,若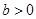 則
則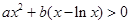 ,故
,故 恒成立,綜上,
恒成立,綜上, 或
或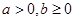 時,函數
時,函數 的圖象恒在函數
的圖象恒在函數 的圖象的上方.
的圖象的上方.
考點:導數的幾何意義,用導數分析函數的單調性,最值,恒成立問題,滲透數形結合思想,分類討論的數學思想


科目:高中數學 來源: 題型:解答題
在自然條件下,某草原上野兔第n年年初的數量記為xn,該年的增長量yn和 xn與 的乘積成正比,比例系數為
的乘積成正比,比例系數為 ,其中m是與n無關的常數,且x1<m,
,其中m是與n無關的常數,且x1<m,
(1)證明: ;
;
(2)用 xn表示xn+1;并證明草原上的野兔總數量恒小于m.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
用總長為14.8m的鋼條制作一個長方體容器的框架,如果所制作容器的底面的一邊比另一邊長0.5m,那么高為多少時容器的容積最大?并求出它的最大容積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某房地產開發商投資81萬元建一座寫字樓,第一年需維護費用為1萬元,以后每年增加2萬元,若把寫字樓出租,每年收入租金30萬元.
(1)開發商最早在第幾年獲取純利潤?
(2)若干年后開發商為了投資其它項目,有兩種處理方案:①純利潤最大時,以10萬元出售該樓;②年平均利潤最大時以46萬元出售該樓.問哪種方案更優?并說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=ax2-2ax+2+b(a≠0),若f(x)在區間[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-mx在[2,4]上單調,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com