Question

甲乙兩班進行消防安全知識競賽，每班出3人組成甲乙兩支代表隊，首輪比賽每人一道必答題，答對則為本隊得1分，答錯不答都得0分，已知甲隊3人每人答對的概率分別為，乙隊每人答對的概率都是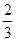．設每人回答正確與否相互之間沒有影響，用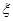表示甲隊總得分．

（I）求隨機變量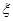的分布列及其數學期望E（）；

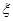（Ⅱ）求在甲隊和乙隊得分之和為4的條件下，甲隊比乙隊得分高的概率．

 

Answer 1

【答案】

（I）如下（Ⅱ）

【解析】

試題分析：解：（1）的可能取值為0，1，2，3

;;

;

的分布列為

	0	1	2	3

 

(2)設“甲隊和乙隊得分之和為4”為事件A,“甲隊比乙隊得分高”為事件B

則;

考點：分布列及其數學期望；概率

點評：求隨機變量的分布列和數學期望是常考題型，解決這種題目關鍵是求出隨機變量對應的概率。