
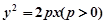 ���^�佹�c(di��n)��б�ʞ�1��
���^�佹�c(di��n)��б�ʞ�1�� ��
�� ���c(di��n)��������
���c(di��n)��������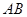 �����c(di��n)�Ŀv
�����c(di��n)�Ŀv ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}

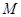 ������(bi��o)��
������(bi��o)��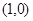 ��
���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
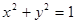 ��
��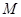 �钁�タ
�钁�タ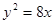 �Ľ��c(di��n)��
�Ľ��c(di��n)��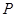 ���O��һ�c(di��n)����
���O��һ�c(di��n)����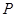 ����O���о��c�A������
����O����c�A������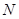 �c(di��n)����
�c(di��n)����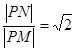
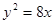 ��(zh��n)��������һ�c(di��n)����A������C���ɗl�о�AB��AC������B��C�����c(di��n).���C��ֱ��BC���^���c(di��n)
��(zh��n)��������һ�c(di��n)����A������C���ɗl�о�AB��AC������B��C�����c(di��n).���C��ֱ��BC���^���c(di��n)�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
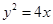 �Ľ��c(di��n)F��ֱ��l�^�c(di��n)
�Ľ��c(di��n)F��ֱ��l�^�c(di��n)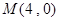 ��
��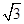 ����ֱ��l��б�ʣ�
����ֱ��l��б�ʣ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
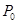 �ǒ��タ
�ǒ��タ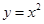 ��һ�c(di��n)�����ڵ�һ����. �^�c(di��n)
��һ�c(di��n)�����ڵ�һ����. �^�c(di��n)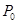 �����タ���о�����
�����タ���о�����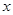 �S��
�S��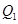 �c(di��n)���^
�c(di��n)���^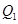 �c(di��n)��
�c(di��n)��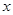 �S�Ĵ����������タ��
�S�Ĵ����������タ��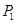 �c(di��n)���˕r�ͷQ
�c(di��n)���˕r�ͷQ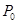 �_����
�_����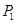 .������ƣ�����
.������ƣ�����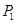 �_��
�_��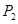 ��
��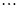 .ӛ
.ӛ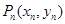 ��
��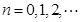 ��
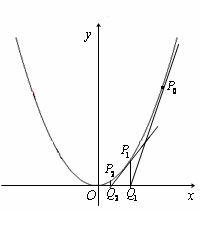
��
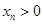 ��
��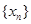 ����{(di��o)�f�p��(sh��)��
����{(di��o)�f�p��(sh��)��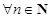 ��
��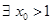 ��ʹ��
��ʹ��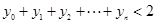 .
.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
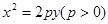 �Ľ��c(di��n)��б�ʞ�1��ֱ���cԓ���タ����A��B���c(di��n)��A��B��
�Ľ��c(di��n)��б�ʞ�1��ֱ���cԓ���タ����A��B���c(di��n)��A��B��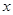 �S�ϵ�����Ӱ�քe��D��C��������ABCD����e��
�S�ϵ�����Ӱ�քe��D��C��������ABCD����e��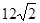 ���t
���t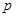 = ��
= ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
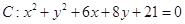 �����タ
�����タ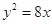 �Ĝ�(zh��n)����
�Ĝ�(zh��n)����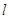 ���O(sh��)���タ������һ�c(di��n)
���O(sh��)���タ������һ�c(di��n)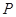 ��ֱ��
��ֱ��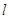 �ľ��x��
�ľ��x��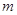 ���t
���t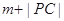 ����Сֵ��
����Сֵ�� �鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
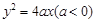 �Ľ��c(di��n)����(bi��o)�ǣ� ��
�Ľ��c(di��n)����(bi��o)�ǣ� ��A����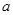 , 0�� , 0�� | B��(��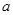 , 0) , 0) | C����0, 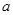 �� �� | D����0, ��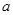 �� �� |
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com