
設n∈N*,不等式組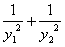 所表示的平面區域為Dn,把Dn內的整點(橫、縱坐標均為整數的點)按其到原點的距離從近到遠排列成點列:(x1,y1),(x2,y2),…,(xn,yn).
所表示的平面區域為Dn,把Dn內的整點(橫、縱坐標均為整數的點)按其到原點的距離從近到遠排列成點列:(x1,y1),(x2,y2),…,(xn,yn).
(1)求(xn,yn);
(2)設數列{an}滿足a1=x1,an=yn2(![]() +
+![]() +…+
+…+![]() )(n≥2),求證:n≥2時,
)(n≥2),求證:n≥2時,![]() ;
;
(3)在(2a)的條件下,比較(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )與4的大小.
)與4的大小.
解:(1)由-nx+2n>0及x>0得0<x<2,因為x∈N*,所以x=1.
又x=1與y=-nx+2n的交點為(1,n),所以Dn內的整點,按由近到遠排列為:
(1,1),(1,2),…,(1,n).
(2)證明:n≥2時,an=yn2(![]() +…+
+…+![]() )=n2[
)=n2[![]() +
+![]() +…+
+…+![]() ].
].
所以![]() =
=![]() +
+![]() +…+
+…+![]() ,
,![]() =
=![]() +
+![]() +…
+…![]() .
.
兩式相減得![]() =
=![]() .
.
(3)n=1時,1+![]() =2<4,n=2時,(1+
=2<4,n=2時,(1+![]() )(1+
)(1+![]() )=
)=![]() <4.
<4.
可猜想:n∈N*時,(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )<4,
)<4,
事實上n≥3時,由(2)知![]() .
.
所以(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )=
)=![]() ·
·![]() ·
·![]() ·…·
·…·![]()
=![]() ·
·![]() ·(
·(![]() ·
·![]() ·…·
·…·![]() )·(1+an)
)·(1+an)
=2·![]() ·(
·(![]() )2·(
)2·(![]() )2·…·(
)2·…·(![]() )2·(
)2·(![]() )2·an+1
)2·an+1
=![]() =2(
=2(![]() +
+![]() +
+![]() +…+
+…+![]() )
)
<2[1+![]() +
+![]() +…+
+…+![]() ]=2(1+1
]=2(1+1![]() +
+![]()
![]() +…+
+…+![]() )<4.
)<4.


科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| y | 2 n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| an+1 | ||
(n+1
|
| an | ||
|
| 1 | ||
|
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年天津一中高三(下)第二次月考數學試卷(理科)(解析版) 題型:解答題
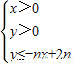 所表示的平面區域為Dn,把Dn內的整點(橫、縱坐標均為整數的點)按其到原點的距離從近到遠排列成點列:(x1,y1),(x2,y2),…,(xn,yn)
所表示的平面區域為Dn,把Dn內的整點(橫、縱坐標均為整數的點)按其到原點的距離從近到遠排列成點列:(x1,y1),(x2,y2),…,(xn,yn)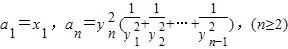 ,求證:n≥2時,
,求證:n≥2時,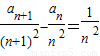 ;
;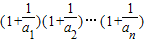 與4的大小.
與4的大小.查看答案和解析>>
科目:高中數學 來源:2007-2008學年浙江省溫州市八校聯考高三(上)期末數學試卷(理科)(解析版) 題型:解答題
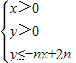 所表示的平面區域為Dn,把Dn內的整點(橫、縱坐標均為整數的點)按其到原點的距離從近到遠排列成點列:(x1,y1),(x2,y2),…,(xn,yn)
所表示的平面區域為Dn,把Dn內的整點(橫、縱坐標均為整數的點)按其到原點的距離從近到遠排列成點列:(x1,y1),(x2,y2),…,(xn,yn)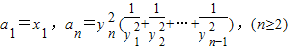 ,求證:n≥2時,
,求證:n≥2時,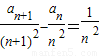 ;
; 與4的大小.
與4的大小.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com