

圖2-2-7
(1)求二面角B-AD-F的大小;
(2)求直線BD與EF所成的角.
解:(1)依題意,因為AD與兩圓所在的平面均垂直,
∴AD⊥AB,AD⊥AF.

故∠BAF為二面角B-AD-F的平面角.
在Rt△ABF中,∠ABF=90°,AF=BC=![]() ,AB=6.
,AB=6.
故cos∠BAF=![]() ,即∠BAF=45°.
,即∠BAF=45°.
∴二面角B-AD-F的大小為45°.
(2)連結(jié)OD,∵OE∥AD,兩圓所在的平面互相平行,故四邊形AOED為平行四邊形.
又OF![]() DE,從而四邊形OFED為平行四邊形,故DO∥EF,
DE,從而四邊形OFED為平行四邊形,故DO∥EF,
∴∠BDO為異面直線BD與EF所成的角(或其補角).
在△DBO中,BD=![]() =10,DO=
=10,DO=![]() ,BO=
,BO=![]() ,
,
BD2=DO2+BO2,故△DBO為直角三角形,從而sin∠BDO=![]() .
.
∴異面直線BD與EF所成的角為arcsin![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
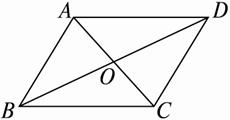
圖2-2-7
A.![]() ,
,![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
求證:△ABC的外心O與A、P、Q四點共圓.

圖2-2-7
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:

圖2-2-7
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com