佛山某中學高三(1)班排球隊和籃球隊各有
名同學,現測得排球隊人的身高(單位:
)分別是:
、
、
、
、
、
、
、
、
、,籃球隊人的身高(單位:)分別是:、
、、
、
、
、
、、
、.
(Ⅰ)請把兩隊身高數據記錄在如圖所示的莖葉圖中,并指出哪個隊的身高數據方差較小(無需計算)；
(Ⅱ)現從兩隊所有身高超過的同學中隨機抽取三名同學,則恰好兩人來自排球隊一人來自籃球隊的概率是多少?
(Ⅰ) 籃球隊的身高數據方差較小；(Ⅱ)
.
解析試題分析：(Ⅰ)用中間的數字表示百位數和十位數，兩邊的數字表示個位數，莖按從小到大的順序（或從大到小的順序）從上向下列出，共莖的葉一般按從大到小（或從小到大）的順序同行列出，從莖葉圖中可以看出籃球隊身高數字較為集中，故方差較小；(Ⅱ) 兩隊所有身高超過的同學恰有
人,其中
人來自排球隊,
人來自籃球隊,分別編號，并列出從人中抽取名同學的基本事件總數，以及恰好兩人來自排球隊、一人來自籃球隊包含的基本事件數，代入古典型的概率計算公式即可.
試題解析：(Ⅰ)莖葉圖如圖所示,籃球隊的身高數據方差較小.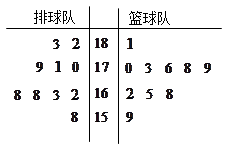
(Ⅱ) 兩隊所有身高超過的同學恰有人,其中人來自排球隊,記為
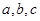,人來自籃球隊,記為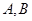
,則從人中抽取名同學的基本事件為:
,
,
,
,
,
,
,
,
,
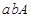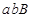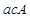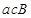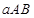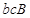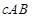共個；其中恰好兩人來自排球隊一人來自籃球隊所含的事件有: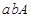,,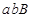,,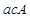,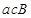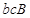共
個, 所以,恰好兩人來自排球隊一人來自籃球隊的概率是
.
考點：1、莖葉圖；2、方差；3、古典概型.
A加金題 系列答案
全優測試卷系列答案科目：高中數學 來源： 題型：解答題
若某產品的直徑長與標準值的差的絕對值不超過1mm時,則視為合格品,否則視為不合格品.在近期一次產品抽樣檢查中,從某廠生產的此種產品中,隨機抽取5000件進行檢測,結果發現有50件不合格品.計算這50件不合格品的直徑長與標準值的差(單位:mm),將所得數據分組,得到如下頻率分布表:
| 分 組 | 頻 數 | 頻 率 |
| [-3,-2) | | 0.10 |
| [-2,-1) | 8 | |
| (1,2] | | 0.50 |
| (2,3] | 10 | |
| (3,4] | | |
| 合計 | 50 | 1.00 |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
對甲、乙兩名自行車賽手在相同條件下進行了6次測試，測得他們的最大速度（m／s）的數據如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
據《中國新聞網》10月21日報道，全國很多省市將英語考試作為高考改革的重點，一時間“英語考試該如何改”引起廣泛關注．為了解某地區學生和包括老師、家長在內的社會人士對高考英語改革的看法，某媒體在該地區選擇了3600人調查（若所選擇的在校學生的人數低于被調查人群總數的80%，則認為本次調查“失效”），就“是否取消英語聽力”的問題，調查統計的結果如下表：
| 應該取消 | 應該保留 | 無所謂 | ||
| 在校學生 | 2100人 | 120人 | y人 | ||
| 社會人士 | 600人 | x人 | z人 |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
根據空氣質量指數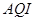
（為整數）的不同，可將空氣質量分級如下表:
| （數值） |  |  |  |  |  |  |
| 空氣質量級別 | 一級 | 二級 | 三級 | 四級 | 五級 | 六級 |
| 空氣質量類別 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
| 空氣質量類別顏色 | 綠色 | 黃色 | 橙色 | 紅色 | 紫色 | 褐紅色 |
年
月
日—月
日，對空氣質量指數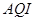進行監測，獲得數據后得到如圖的條形圖
天計）空氣質量類別為中度污染的概率；
個，求至少有一個數據反映的空氣質量類別顏色為褐紅色的概率.查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某工廠有25周歲以上(含2S周歲)工人300名，25周歲以下工人200名為研究工人的日平均生產量是否與年齡有關，現采用分層抽樣的方法，從中抽取了100名工人，先統計了他們某月的日平均生產件數，然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組，再將兩組工人的日平均生產件數分成5組：[50,60), [60,70), [70,80), [80,90), [90,100), 分別加以統計，得到如圖所示的頻率分布直方圖。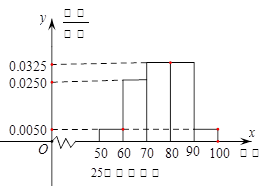
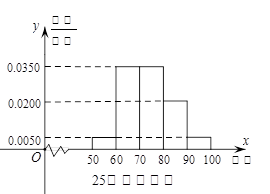
(1)求樣本中“25周歲以上(含25周歲)組”抽取的人數、日生產量平均數；
(2)若“25周歲以上組”中日平均生產90件及90件以上的稱為“生產能手”；“25周歲以下組”中日平均生產不足60件的稱為“菜鳥”。從樣本中的“生產能手”和”菜鳥”中任意抽取2人，求這2人日平均生產件數之和X的分布列及期望。(“生產能手”日平均生產件數視為95件，“菜鳥”日平均生產件數視為55件)。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某英語學習小組共12名同學進行英語聽力測試，隨機抽取6名同學的測試成績（單位：分），用莖葉圖記錄如下，其中莖為十位數，葉為個位數.
（1）根據莖葉圖計算樣本均值；
（2）成績高于樣本均值的同學為優秀，根據莖葉圖估計該小組12名同學中有幾名優秀同學；
（3）從該小組12名同學中任取2人，求僅有1人是來自隨機抽取6人中優秀同學的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
為預防H7N9病毒爆發，某生物技術公司研制出一種新流感疫苗，為測試該疫苗的有效性（若疫苗有效的概率小于90%，則認為測試沒有通過），公司選定2000個流感樣本分成三組，測試結果如下表：
| 分組 | A組 | B組 | C組 |
| 疫苗有效 | 673 | a | b |
| 疫苗無效 | 77 | 90 | c |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
為了對某課題進行研究，用分層抽樣方法從三所科研單位A、B、C的相關人員中，抽取若干人組成研究小組，有關數據見下表（單位：人）：
| 科研單位 | 相關人數 | 抽取人數 |
| A | 16 |  |
| B | 12 | 3 |
| C | 8 |  |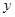
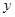與的值；查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com