已知平面
α⊥平面
β,交線為
AB,
C∈

,
D∈

,

,
E為
BC的中點,
AC⊥
BD,
BD=8.

①求證:
BD⊥平面

;
②求證:平面
AED⊥平面
BCD;
③求二面角
B-
AC-
D的正切值.
①
AB是
AC在平面
β上的射影,由
AC⊥
BD得
AB⊥
BD.∵
α⊥
β.∴
DB⊥
α.
②由
AB=
AC,且
E是
BC中點,得
AE⊥
BC,又
AE⊥
DB,故
AE⊥平面
BCD,因此可證得平面
AED⊥平面
BCD.
③設(shè)
F是
AC中點,連
BF,
DF.由于△
ABC是正三角形,故
BF⊥
AC.又由
DB⊥平面
α,則
DF⊥
AC,∠
BFD是二面角
B-
AC-
D的平面角,
在Rt△
BFD中,
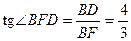
.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,四棱錐

的底面是邊長為1的正方形,

底面

,

。

(1)求證:

;
(2)設(shè)棱
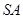
的中點為

,求異面直線

與

所成角的大小;
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題共14分)
四棱錐P—ABCD中,PA⊥底面ABCD,AB//CD,AD=CD=1,∠BAD=120°,PA=

,∠ACB=90°。
(I)求證:BC⊥平面PAC;
(II)求二面角D—PC—A的大小;
(III)求點B到平面PCD的距離。

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
棱長為1的正方體

的8個頂點都在球

的表面上,

分別
是棱

,

的中點,則直線

被球

截得的線段長為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
(改編題)

如圖,直三棱柱

中,

,

上有一動點

,則

周長的最小值為
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知異面直線l1和l2,l1⊥l2,MN是l1和l2的公垂線,MN = 4,A∈l1,B∈l2,AM = BN = 2,O是MN中點.①求l1與OB的成角.②求A點到OB距離.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
四棱錐P-ABCD的底面是矩形,側(cè)面PAD是正三角形,且側(cè)面PAD

底面ABCD,當(dāng)
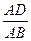
的值等于多少時,能使PB

AC?并給出證明.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知
a、
b為直線,α、β為平面.在下列四個命題中,
① 若
a⊥α,
b⊥α,則
a∥
b; ② 若
a∥α,
b ∥α,則
a∥
b;
③ 若
a⊥α,
a⊥β,則α∥β; ④ 若α∥
b,β∥
b,則α∥β.
正確命題的個數(shù)是
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
在四棱錐
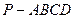
中,

平面

,底面

為矩形,

.
(I)當(dāng)
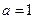
時,求證:
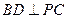
;
(II)若

邊上有且只有一個點

,使得

,求此時二面角

的余弦值.

查看答案和解析>>

 ,D∈
,D∈ ,
, ,E為BC的中點,AC⊥BD,BD=8.
,E為BC的中點,AC⊥BD,BD=8.
 ;
; ,∠ACB=90°。
,∠ACB=90°。
 底面ABCD,當(dāng)
底面ABCD,當(dāng)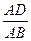 的值等于多少時,能使PB
的值等于多少時,能使PB AC?并給出證明.
AC?并給出證明.
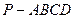 中,
中, 平面
平面 ,底面
,底面 為矩形,
為矩形, .
.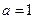 時,求證:
時,求證: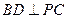 ;
; 邊上有且只有一個點
邊上有且只有一個點 ,使得
,使得 ,求此時二面角
,求此時二面角 的余弦值.
的余弦值.