
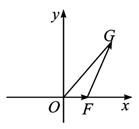
(1)求x0關于t的函數x0=f(t)的表達式,判斷函數f(t)的單調性,并證明你的判斷;
(2)設△OFG的面積S=![]() t,若以O為中心、F為焦點的橢圓經過點G,求當|
t,若以O為中心、F為焦點的橢圓經過點G,求當|![]() |取得最小值時橢圓的方程.
|取得最小值時橢圓的方程.
解:(1)由題意知![]() =(x0-t,y0),
=(x0-t,y0), ![]() =(t,0),則
=(t,0),則![]() ·
·![]() =t(x0-t)=1.
=t(x0-t)=1.
解得x0=f(t)=t+![]() .
.
設t1>t2≥3,則f(t1)-f(t2)=(t1+![]() )-(t2+
)-(t2+![]() )=(t1-t2)-
)=(t1-t2)-![]() =(t1-t2)
=(t1-t2)![]() .
.
∵t1-t2>0,t1t2-1>0,t1t2>0,
∴f(t1)-f(t2)>0,f(t1)>f(t2),函數f(t)在區間[3,+∞]上單調遞增.
(2)由S=![]() |
|![]() ||y0|=
||y0|=![]() ×t×|y0|=
×t×|y0|=![]() t,得y0=±
t,得y0=±![]() .
.
∴點G的坐標為(t+![]() ,±
,±![]() ),|
),|![]() |2=(t+
|2=(t+![]() )2+
)2+![]() .
.
∵函數f(t)在區間[3,+∞]上單調遞增,
∴當t=3時,| ![]() |取得最小值,此時點F、G的坐標分別為(3,0)、(
|取得最小值,此時點F、G的坐標分別為(3,0)、(![]() ,±
,±![]() ).
).
由題意設橢圓方程為![]() +
+![]() =1.
=1.
由點G在橢圓上,得![]() +
+![]() =1,
=1,
解得b2=9.
∴所求橢圓方程為![]() +
+![]() =1.
=1.


科目:高中數學 來源: 題型:
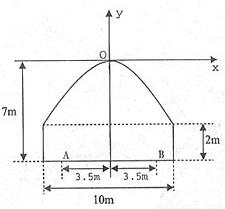
 如圖所示,一隧道內設雙行線公路,其截面由長方形的三條邊和拋物線的一段構成,為保證安全,要求行駛車輛頂部(設為平頂)與隧道頂部在豎直方向上高度之差至少要有0.5米.
如圖所示,一隧道內設雙行線公路,其截面由長方形的三條邊和拋物線的一段構成,為保證安全,要求行駛車輛頂部(設為平頂)與隧道頂部在豎直方向上高度之差至少要有0.5米.查看答案和解析>>
科目:高中數學 來源:2008-2009學年福建省泉州市惠安縣惠南中學高二(上)期末數學試卷(選修2-1)(理科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com