
設不等式 的解集為M.
的解集為M.
(1)如果 ,求實數
,求實數 的取值范圍;
的取值范圍;
(2)如果 ,求實數
,求實數 的取值范圍.
的取值范圍.
(1)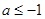 或
或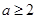 ;(2)
;(2)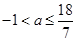 .
.
解析試題分析:本題考查含參一元二次不等式的解法及二次函數圖像的性質等基礎知識,考查轉化思想、分類討論思想等數學思想方法.第一問,由于拋物線開口向上,要使不等式的解集不為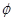 ,只需
,只需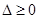 ;第二問,一元二次不等式含參數
;第二問,一元二次不等式含參數 ,對應的一元二次方程是否有解取決于
,對應的一元二次方程是否有解取決于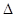 ,所以本問討論
,所以本問討論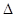 的三種情況,在每一種情況下,求出方程的根,寫出不等式的解集,利用子集關系列出不等式,求
的三種情況,在每一種情況下,求出方程的根,寫出不等式的解集,利用子集關系列出不等式,求 的取值范圍.
的取值范圍.
試題解析:(1)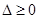 ,
,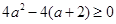 ,∴
,∴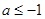 或
或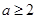 . 4分
. 4分
(2)①當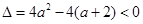 ,即
,即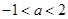 時,
時,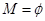 ,滿足題意; 6分
,滿足題意; 6分
②當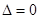 時,
時,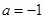 或
或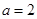 ,
,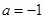 時,
時,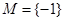 ,不合題意;
,不合題意;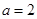 時,
時,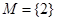 ,滿足題意; 8分
,滿足題意; 8分
③當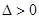 ,即
,即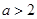 或
或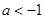 時,令
時,令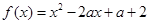 ,要使
,要使 ,只需
,只需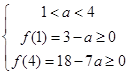 , 10分
, 10分
得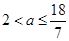 ,綜上,
,綜上,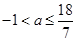 . 12分
. 12分
考點:1.二次函數的判別式;2.含參一元二次不等式的解法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
如圖是某重點中學學校運動場平面圖,運動場總面積15000平方米,運動場是由一個矩形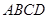 和分別以
和分別以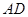 、
、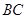 為直徑的兩個半圓組成,塑膠跑道寬8米,已知塑膠跑道每平方米造價為150元,其它部分造價每平方米80元,
為直徑的兩個半圓組成,塑膠跑道寬8米,已知塑膠跑道每平方米造價為150元,其它部分造價每平方米80元,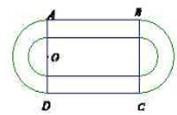
(Ⅰ)設半圓的半徑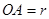 (米),寫出塑膠跑道面積
(米),寫出塑膠跑道面積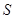 與
與 的函數關系式
的函數關系式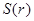 ;
;
(Ⅱ)由于受運動場兩側看臺限制, 的范圍為
的范圍為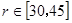 ,問當
,問當 為何值時,運動場造價最低(第2問
為何值時,運動場造價最低(第2問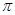 取3近似計算).
取3近似計算).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數 ,且不等式
,且不等式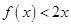 的解集為
的解集為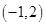 .
.
(1)方程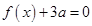 有兩個相等的實根,求
有兩個相等的實根,求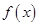 的解析式;
的解析式;
(2)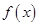 的最小值不大于
的最小值不大于 ,求實數
,求實數 的取值范圍;
的取值范圍;
(3) 如何取值時,函數
如何取值時,函數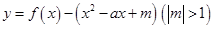 存在零點,并求出零點.
存在零點,并求出零點.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 ,
, ,其中實數
,其中實數 .
.
(1)若 ,求函數
,求函數 的單調區間;
的單調區間;
(2)當函數 與
與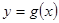 的圖象只有一個公共點且
的圖象只有一個公共點且 存在最小值時,記
存在最小值時,記 的最小值為
的最小值為 ,求
,求 的值域;
的值域;
(3)若 與
與 在區間
在區間 內均為增函數,求實數
內均為增函數,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com