
 ,求f(x)的單調增區間;
,求f(x)的單調增區間; ,求ω的值.
,求ω的值. ,把
,把 代入函數解析式,得到的函數值f(
代入函數解析式,得到的函數值f(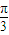 )為函數的最值,從而得到
)為函數的最值,從而得到 ,根據余弦函數的圖象與性質得
,根據余弦函數的圖象與性質得
 時,
時, ,(2分)
,(2分) ,
,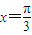 ,
, 取最值,
取最值, ,(8分)
,(8分) (k∈Z),
(k∈Z), ,(10分)
,(10分) .(12分)
.(12分)

 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com