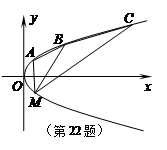(12分)(已知拋物線
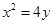
,過定點
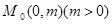
的直線
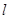
交拋物線于A、B兩點.
(Ⅰ)分別過A、B作拋物線的兩條切線,A、B為切點,求證:這兩條切線的交點
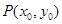
在定直線
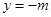
上.
(Ⅱ)當

時,在拋物線上存在不同的兩點P、Q關于直線
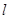
對稱,弦長|PQ|中是否存在最大值?若存在,求其最大值(用
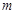
表示),若不存在,請說明理由.
(Ⅰ)由
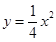
,得

,設
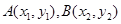
過點A的切線方程為:

,即
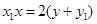
同理求得過點B的切線方程為:
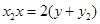
∵直線PA、PB過
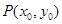
,∴
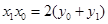
,
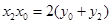
∴點
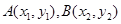
在直線
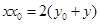
上,∵直線AB過定點
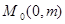
,
∴
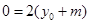
,即
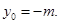
∴兩條切線PA、PB的交點
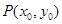
在定直線
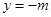
上.
(Ⅱ)設
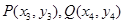
,設直線
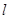
的方程為:
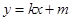
,
則直線
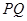
的方程為:
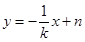
,
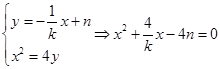
,
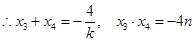
,
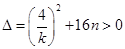
①
設弦PQ的中點
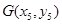
,則
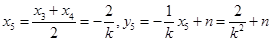
∵弦PQ的中點
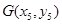
在直線
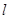
上,∴
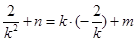
,
即
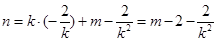
②
②代入①中,得
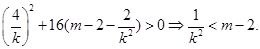
③
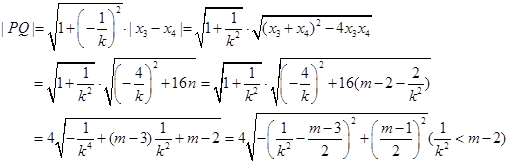
由已知

,當
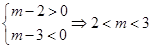
時,弦長|PQ|中不存在最大值.
當
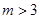
時,這時
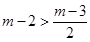
,此時,弦長|PQ|中存在最大值,
即當
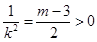
時,弦長|PQ|中的最大值為略
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
直線
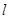
與拋物線
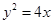
交于
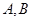
兩點,
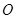
為原點,如果
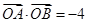
,那么直線
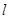
恒經(jīng)過定點
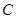
的坐標為__________________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若直線
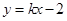
與拋物線
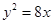
交于
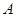
、
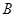
兩點,若線段
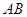
的中點的橫坐標是
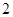
,則
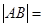 .
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
過原點O引拋物線
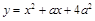
的切線,當
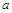
變化時,兩個切點分別在拋物線( )上
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若拋物線
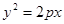
的焦點與雙曲線
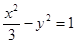
的右焦點重合,則p的值為()
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若拋物線
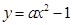
上總存在兩點關于直線
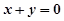
對稱,則實數(shù)
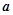
的取值范圍是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
拋物線

上縱坐標為

的點

到焦點的距離為2.
(Ⅰ)求
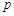
的值;
(Ⅱ)如圖,

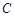
為拋物線上三點,且線段
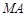
,

,
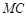
與
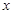
軸交點的橫坐標依次組成公差為1的等差數(shù)列,若
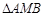
的面積是
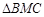
面積的
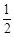
,求直線

的方程.
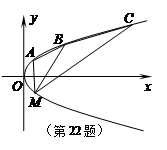
查看答案和解析>>

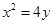 ,過定點
,過定點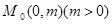 的直線
的直線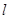 交拋物線于A、B兩點.
交拋物線于A、B兩點.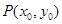 在定直線
在定直線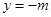 上.
上. 時,在拋物線上存在不同的兩點P、Q關于直線
時,在拋物線上存在不同的兩點P、Q關于直線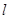 對稱,弦長|PQ|中是否存在最大值?若存在,求其最大值(用
對稱,弦長|PQ|中是否存在最大值?若存在,求其最大值(用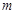 表示),若不存在,請說明理由.
表示),若不存在,請說明理由. 上縱坐標為
上縱坐標為 的點
的點 到焦點的距離為2.
到焦點的距離為2.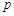 的值;
的值;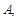

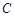 為拋物線上三點,且線段
為拋物線上三點,且線段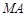 ,
, ,
,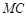 與
與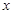 軸交點的橫坐標依次組成公差為1的等差數(shù)列,若
軸交點的橫坐標依次組成公差為1的等差數(shù)列,若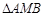 的面積是
的面積是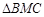 面積的
面積的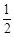 ,求直線
,求直線 的方程.
的方程.