函數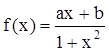
是定義在
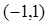上的奇函數，且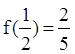
（1）確定函數
的解析式。
（2）用定義法證明
在
上是增函數。
（3）解關于t的不等式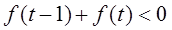
千里馬走向假期期末仿真試卷寒假系列答案科目：高中數學 來源： 題型：解答題
（本小題滿分12分）
設平面直角坐標系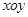
中，設二次函數
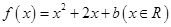的圖象與兩坐標軸有三個交點，經過這三個交點的圓記為
．求：
（Ⅰ）求實數
的取值范圍；
（Ⅱ）求圓的方程；
（Ⅲ）問圓是否經過某定點（其坐標與b 無關）？請證明你的結論．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（14分）病人按規定的劑量服用某藥物，測得服藥后，每毫升血液中含藥量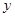
（毫克）與時間
（小時）滿足：前1小時內成正比例遞增，1小時后按指數型函數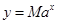
（
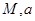為常數）衰減．如圖是病人按規定的劑量服用該藥物后，每毫升血液中藥物含量隨時間變化的曲線．
（1）求函數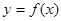
的解析式；
（2）已知每毫升血液中含藥量不低于0.5毫克時有治療效果，低于0.5毫克時無治療效果．求病人一次服藥后的有效治療時間為多少小時？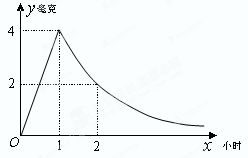
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本題滿分13分）
為了保護環境，某工廠在政府部門的支持下，進行技術改進： 把二氧化碳轉化為某種化工產品，經測算，該處理成本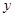
（萬元）與處理量
（噸）之間的函數關系可近似地表示為：
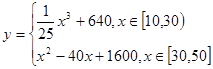， 且每處理一噸二氧化碳可得價值為
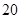萬元的某種化工產品.
(Ⅰ)當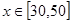
時，判斷該技術改進能否獲利？如果能獲利，求出最大利潤；如果不能獲利，則國家至少需要補貼多少萬元，該工廠才不虧損？
（Ⅱ） 當處理量為多少噸時，每噸的平均處理成本最少.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
（2）
在
上是增函數。（3）
。
的不等式：
,求函數
最大值和最小值;
有兩根
，試求
的值.
=
(
)的圖像經過點(2，
)，其中a>0且a
1.
，方程
的兩根
和
滿足
．
的取值范圍；
與
的大小．并說明理由．