
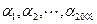 為2008個整數,且
為2008個整數,且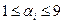 (
(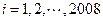 )。如果存在某個
)。如果存在某個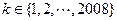 ,使得2008位數
,使得2008位數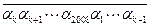 被101整除,試證明:對一切
被101整除,試證明:對一切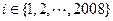 ,2008位數
,2008位數 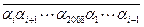 均能被101整除。
均能被101整除。科目:高中數學 來源:不詳 題型:解答題
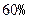 (即衰變了
(即衰變了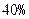 ),該動物大約在距今多少年前死亡?
),該動物大約在距今多少年前死亡?查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
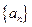 滿足,
滿足,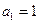 ,
,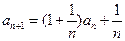 (n∈N*)。
(n∈N*)。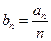 ,求數列
,求數列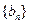 的通項公式;
的通項公式;查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
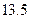 萬元的新車,專家預測這種車每年按
萬元的新車,專家預測這種車每年按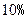 的速度折舊.
的速度折舊.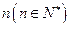 年后這輛車的價值.
年后這輛車的價值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com