中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

（本題滿分14分）

      對于函數，若存在成立，則稱的不動點.如果函數

有且只有兩個不動點0，2，且

      （1）求函數的解析式；

      （2）已知各項不為零的數列，求數列通項；

      （3）如果數列滿足，求證：當時，恒有成立.

（本小題滿分14分）

解：設得：由違達定理得：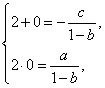

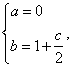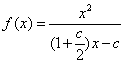解得代入表達式，由

得不止有兩個不動點，

………………………………………5分

（2）由題設得     （A）

且          （B）

由（A）（B）得：

解得（舍去）或；由，若這與矛盾，

，即{是以1為首項，1為公差的等差數列，

；     ………………………………………………………………10分

（3）證法（一）：運用反證法，假設則由（1）知

∴，而當

這與假設矛盾，故假設不成立，∴.………………………………………14分

證法（二）：由

得<0或結論成立；

若，此時從而

即數列{}在時單調遞減，由，可知上成立.………………………………………………………………………………………14分

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

（本題滿分14分
A．選修4-4：極坐標與參數方程在極坐標系中，直線l 的極坐標方程為θ=
π
3
 （ρ∈R ），以極點為坐標原點，極軸為x軸的正半軸建立平面直角坐標系，曲線C的參數方程為
x=2cosα
y=1+cos2α
 （α 參數）．求直線l 和曲線C的交點P的直角坐標．
B．選修4-5：不等式選講
設實數x，y，z 滿足x+y+2z=6，求x2+y2+z2 的最小值，并求此時x，y，z 的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

（本題滿分14分）如圖，四邊形ABCD為矩形，AD⊥平面ABE，AE＝EB＝BC＝2，為上的點，且BF⊥平面ACE．

（1）求證：AE⊥BE；（2）求三棱錐D－AEC的體積；（3）設M在線段AB上，且滿足AM＝2MB，試在線段CE上確定一點N，使得MN∥平面DAE.

查看答案和解析>>

科目：高中數學 來源：2011-2012學年江蘇省高三上學期期中考試數學 題型：解答題

(本題滿分14分)已知集合A={x|x2-2x-3≤0，x∈R}，B={x|x2-2mx+m2-4≤0，x∈R，m∈R}

(Ⅰ)若AB=[0,3]，求實數m的值

(Ⅱ)若ACRB，求實數m的取值范圍

 

查看答案和解析>>

科目：高中數學 來源：2010-2011學年福建省高三上學期第三次月考理科數學卷 題型：解答題

(本題滿分14分)

已知點是⊙：上的任意一點，過作垂直軸于,動點滿足。

（1）求動點的軌跡方程； 

（2）已知點，在動點的軌跡上是否存在兩個不重合的兩點、，使 (O是坐標原點)，若存在，求出直線的方程，若不存在，請說明理由。

 

查看答案和解析>>

科目：高中數學 來源：2014屆江西省高一第二學期入學考試數學 題型：解答題

(本題滿分14分)已知函數.

(1)求函數的定義域；

(2)判斷的奇偶性；

(3)方程是否有根?如果有根，請求出一個長度為的區間，使

；如果沒有，請說明理由?(注：區間的長度為).

 

查看答案和解析>>

同步練習冊答案