有下列命題:①若四邊形的四邊相等,則這個四邊形一定菱形;②在正方體
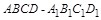
中,分別是棱
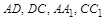
的中點,則直線
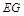
與
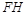
一定相交,且交點在直線
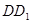
上;③若點
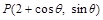
,
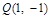
,則
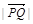
的最大值是
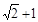
;④若
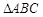
的頂點A、B分別是橢圓
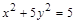
兩個焦點,且滿足
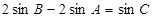
,則頂點C的軌跡方程是雙曲線.
其中所有正確命題的序號是
.
試題分析:①四邊形有可能是空間四邊形;②根據(jù)公理3可知正確;
③
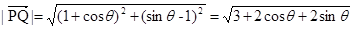

,所以最大值為
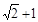
;
④因為
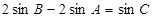
,所以由正弦定理,容易得到:|CB|-|CA|=
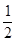
|AB|。
因為A、B分別是橢圓
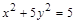
的左、右焦點,所以|AB|為定值,即
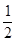
|AB|為定值,
所以點C的軌跡是以A、B為焦點,
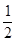
|AB|為實軸長的雙曲線右半支。
點評:如①如果放在同一平面內,則為真命題,在空間中則為假命題,是本題的易忽略點。一般的,在平面上經(jīng)常見到的說法正確到空間中不一定成立;在運用雙曲線的定義時,應特別注意定義中的條件:差的絕對值。弄清是指整條雙曲線還是雙曲線的一支以及是哪一支。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
設
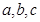
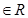
,則“2b=a+c”是“a,b,c三個數(shù)成等差數(shù)列”的
| A.充分而不必要條件 | B.必要而不充分條件 |
| C.充分必要條件 | D.既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
命題“
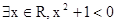
”的否定是______________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分12分)
已知命題
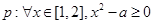
.命題
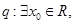
使得
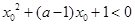
;若“
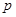
或
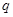
為真,
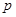
且
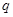
為假”,求實數(shù)
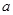
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若p是真命題,q是假命題。以下四個命題 ① p且q ② p或q ③ 非p ④非q。
其中假命題的個數(shù)是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
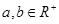
,那么“
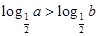
”是 “
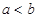
”的( )
| A.充要條件 | B.充分不必要條件 |
| C.必要不充分條件 | D.既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若命題“
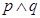
”為假,且
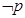
為假,則( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(10分)命題
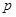
:關于
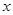
的不等式
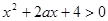
,對一切
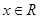
恒成立,命題
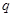
:函數(shù)
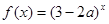
是增函數(shù),若
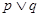
為真,
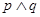
為假,求實數(shù)
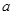
的取值范圍.
查看答案和解析>>

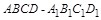
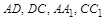 的中點,則直線
的中點,則直線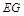 與
與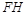 一定相交,且交點在直線
一定相交,且交點在直線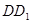 上;③若點
上;③若點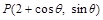 ,
,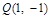 ,則
,則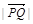 的最大值是
的最大值是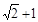 ;④若
;④若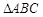 的頂點A、B分別是橢圓
的頂點A、B分別是橢圓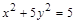 兩個焦點,且滿足
兩個焦點,且滿足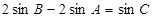 ,則頂點C的軌跡方程是雙曲線.
,則頂點C的軌跡方程是雙曲線.
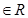 ,則“2b=a+c”是“a,b,c三個數(shù)成等差數(shù)列”的
,則“2b=a+c”是“a,b,c三個數(shù)成等差數(shù)列”的