
(1)若P1、P2點的橫坐標分別為x1、x2,則x1、x2之間滿足怎樣的關系?并證明你結論;
(2)求雙曲線E的方程;
(3)設雙曲線E上的動點M,兩焦點為F1,F2,若MF1與MF2的夾角為鈍角,求M點橫坐標x0的取值范圍.

解:(1)由e2=![]() =1+(
=1+(![]() )2=(
)2=(![]() )2,得
)2,得![]() =
=![]() .
.
∴兩漸近線OP1、OP2的方程分別為y=![]() x和y=-
x和y=-![]() x.
x.
設點P1(x1,![]() x1)、點P2(x2,-
x1)、點P2(x2,-![]() x).
x).
設∠P1OP2=2α,則tanα=![]() ,∴sin2α=
,∴sin2α=![]()
cos2α=![]()
又S△OP1P2=![]() |
|![]() ||
||![]() |sin2α=
|sin2α=![]() ·|
·|![]() ||
||![]() |=
|=![]() ,
,
∴|![]() ||
||![]() |=
|=![]() .
.
∴![]() ·
·![]() =|
=|![]() ||
||![]() |cos2α=
|cos2α=![]() ×(
×(![]() )=
)=![]() =x1x2
=x1x2![]() x1x2=
x1x2=![]() ·x1x2,即x1x2=
·x1x2,即x1x2=![]() .
.
(2)由點P為線段![]() 的一個三等分點可知,點P分
的一個三等分點可知,點P分![]() 所成的比λ=2,
所成的比λ=2,
∴P點坐標為(![]() ),即(
),即(![]() ).
).
設P(x,y),則x=![]() 且y=
且y=![]() ,即x1+2x2=3x且x1-2x2=2y,
,即x1+2x2=3x且x1-2x2=2y,
∴(3x)2-(2y)2=(x1+2x2)2-(x1-2x2)2=8x1x2=36,即![]() =1.
=1.
(3)由(2)知c=![]() ,∴F1(
,∴F1(![]() ,0),
,0),
F2(![]() ,0),y02=
,0),y02=![]() -9,
-9,
∴![]() ·
·![]() =|
=|![]() ||
||![]() |cos<
|cos<![]() ,
,![]() >=(
>=(![]() -x0,-y0)·(
-x0,-y0)·(![]() -x0,-y0)=x02-13+y02=x02-13+
-x0,-y0)=x02-13+y02=x02-13+![]() -9=
-9=![]() -22<0,即|x0|<
-22<0,即|x0|<![]() .
.
又|x0|>2,
故x0的取值范圍為(-![]() ,-2)∪(2,
,-2)∪(2,![]() ).
).


科目:高中數學 來源: 題型:
 如圖,已知橢圓C:
如圖,已知橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| F1A |
| F2A |
| π |
| 3 |
| 2π |
| 3 |
4
| ||
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•荊門模擬)如圖,已知直線OP1,OP2為雙曲線E:
(2013•荊門模擬)如圖,已知直線OP1,OP2為雙曲線E:| x2 |
| a2 |
| y2 |
| b2 |
| 27 |
| 4 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北省荊門市高三元月調考文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)如圖,已知直線OP1,OP2為雙曲線E: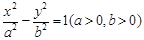 的漸近線,△P1OP2的面積為
的漸近線,△P1OP2的面積為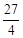 ,在雙曲線E上存在點P為線段P1P2的一個三等分點,且雙曲線E的離心率為
,在雙曲線E上存在點P為線段P1P2的一個三等分點,且雙曲線E的離心率為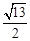 .
.
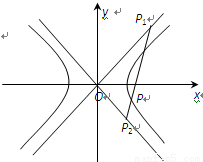
(1)若P1、P2點的橫坐標分別為x1、x2,則x1、x2之間滿足怎樣的關系?并證明你的結論;
(2)求雙曲線E的方程;
(3)設雙曲線E上的動點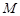 ,兩焦點
,兩焦點 ,若
,若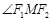 為鈍角,求
為鈍角,求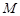 點橫坐標
點橫坐標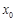 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com