分析:(1)f
1(x)∉M,不妨令f
1(x)∈M,則存在x
0,使
=+1,解此方程,若方程有解,則說明假設成立f
1(x)∈M,否則說明不成立;
(2)f
2(x)∈M.不妨令g(x)=f
2(x+1)-f
2(x)-f
2(1),代入解析式進行判斷,若此函數有零點,則說明函數f
2=2
x+x
2屬于集合M,否則說明它不屬于集合M;
(3)函數
f3(x)=lg∈M,則存在x
0,使得
lg=
lg+lg,由于本題要求出一個滿足要求的實數a的值,可從此方程中將a表示為x
0的函數,得到a=
,利用導數解出此函數的最值,即可得出函數的值域,即a可以存在的范圍,從中任意找出一個值即可.
解答:解:(1)由題意,f
1(x)∉M.
假若f
1(x)∈M,則存在x
0,使
=+1,
得x
02+x
0+1=0.此方程無解,
故f
1(x)∉M.
(2)由題意f
2(x)∈M.
令g(x)=f
2(x+1)-f
2(x)-f
2(1)=2
x+1+(x+1)
2-2
x-x
2-2-1=2(2
x-1+x-1),
由于g(0)=-1,g(1)=2,
故函數f
2(x)在(0,1)上至少有一個零點,
設為x
0,它滿足f
2(x
0+1)=f
2(x
0)+f
2(1),
所以f
2(x)∈M.
(3)由于
f3(x)=lg∈M,
得存在x
0,使得
lg=
lg+lg,即
=
×,
所以a=
,
令g(x)=
,
g′(x)=
=0,得x=
,
結合如圖的圖象,函數g(x)在(-∞,
)上單調增,在(
,)上單調減,在(
,+∞)上單調增,且x<-1時g(x)>2,x>2時g(x)<2,
所以g(x)的值域為[3-
,3+
],
于是a∈[3-
,3+
].
可取a=3
點評:本考查函數與方程的綜合運用,考查了分式方程的解法,函數零點的判定定理,解對數方程,利用導數求最值,解題的關鍵是理解題設中所給的定義,理解其運算規則,由此得到方程,再由函數的相關知識綜合作出判斷本題綜合性強,尤其是第三小題的求解,需要構造函數研究參數的取值范圍,用到了函數的思想,這是本題的難點,做題時根據問題選擇合適的工具可以大大降低解題的難度



 優等生題庫系列答案
優等生題庫系列答案 53天天練系列答案
53天天練系列答案![]() f(x0+1)=f(x0)+f(1)成立.
f(x0+1)=f(x0)+f(1)成立.![]() 是否屬于集合M?說明理由;
是否屬于集合M?說明理由;![]() ,求實數a的取值范圍;
,求實數a的取值范圍;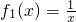 是否屬于集合M?說明理由.
是否屬于集合M?說明理由.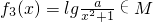 ,試給出一個滿足要求的實數a的值.
,試給出一個滿足要求的實數a的值.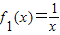 是否屬于集合M?說明理由.
是否屬于集合M?說明理由.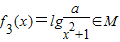 ,試給出一個滿足要求的實數a的值.
,試給出一個滿足要求的實數a的值.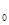 ,使得
,使得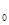 +1)=f(x
+1)=f(x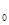 )+f(1)成立。
)+f(1)成立。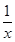 是否屬于集合M?說明理由;
是否屬于集合M?說明理由;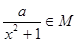 ,求實數a的取值范圍;
,求實數a的取值范圍;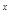 +x
+x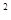
 M。
M。