
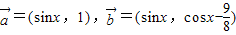 ,設函數
,設函數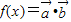 ,x∈[0,π]
,x∈[0,π]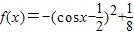 ,由此函數是一個復合函數,分類討論cosx的取值范圍,利用復合函數的單調性的判斷規則判斷出單調性區間;
,由此函數是一個復合函數,分類討論cosx的取值范圍,利用復合函數的單調性的判斷規則判斷出單調性區間;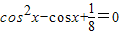 有兩個根,此兩根為cosα,cosβ,由根與系數的關系
有兩個根,此兩根為cosα,cosβ,由根與系數的關系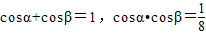 ,再由由到角三角函數關系,解出
,再由由到角三角函數關系,解出 易求cos(α+β)的值;
易求cos(α+β)的值;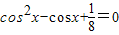 有兩個根,此兩根為cosα,cosβ,解一元二次方程
有兩個根,此兩根為cosα,cosβ,解一元二次方程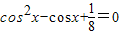 可得出cosα,cosβ的值,再解出兩角的正弦值,代入cos(α+β)的展開式,即可求cos(α+β)的值
可得出cosα,cosβ的值,再解出兩角的正弦值,代入cos(α+β)的展開式,即可求cos(α+β)的值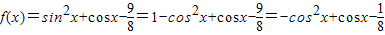
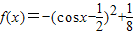
 時,
時, ,且t=cosx為減函數
,且t=cosx為減函數 在
在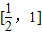 上時減函數,
上時減函數,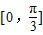 上是增函數
上是增函數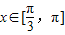 時,
時,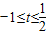 ,且t=cosx為減函數
,且t=cosx為減函數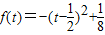 在
在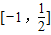 上時增函數,
上時增函數, 上是減函數
上是減函數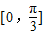 ,
,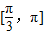
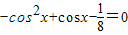 ,即
,即
 的兩個根,從而
的兩個根,從而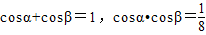

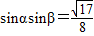 ,
,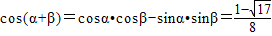
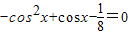 ,即
,即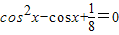
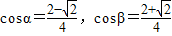 ,
,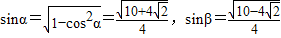 ,
,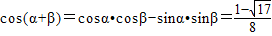


科目:高中數學 來源:浙江省瑞安中學2011-2012學年高一下學期期末考試數學文科試題 題型:044
已知向量![]() ,設函數f(x)=a·b其中x∈R.
,設函數f(x)=a·b其中x∈R.
(1)求函數f(x)的最小正周期和單調遞增區間.
(2)將函數f(x)的圖象的縱坐標保持不變,橫坐標擴大到原來的兩倍,然后再向右平移![]() 個單位得到g(x)的圖象,求g(x)的解析式.
個單位得到g(x)的圖象,求g(x)的解析式.
查看答案和解析>>
科目:高中數學 來源:2013年普通高等學校招生全國統一考試陜西卷文數 題型:044
已知向量![]() ,設函數f(x)=a·b.
,設函數f(x)=a·b.
(Ⅰ)求f(x)的最小正周期.
(Ⅱ)求f(x)在[0,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源:2014屆浙江省高一下學期期末考試文科數學試卷(解析版) 題型:解答題
已知向量 ,設函數
,設函數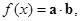 其中xÎR.
其中xÎR.
(1)求函數 的最小正周期和單調遞增區間.
的最小正周期和單調遞增區間.
(2)將函數 的圖象的縱坐標保持不變,橫坐標擴大到原來的兩倍,然后再向右平移
的圖象的縱坐標保持不變,橫坐標擴大到原來的兩倍,然后再向右平移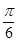 個單位得到
個單位得到 的圖象,求
的圖象,求 的解析式.
的解析式.
查看答案和解析>>
科目:高中數學 來源:天津模擬題 題型:解答題
 ,設函數f(x)=m·n-1,
,設函數f(x)=m·n-1,  ,求
,求 的值.
的值. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com