
 的前三項分別為
的前三項分別為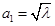 ,
,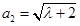 ,
,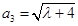 ,(其中
,(其中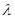 為正常數)。設
為正常數)。設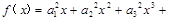
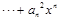 。
。 的通項公式,并證明數列
的通項公式,并證明數列 不可能為等比數列;
不可能為等比數列;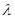 =1,求
=1,求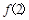 的值;
的值;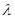 =4,試證明:當
=4,試證明:當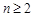 時,
時,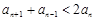 .
.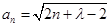 ,證明詳見解析;(2)
,證明詳見解析;(2)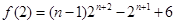 ;(3)詳見解析.
;(3)詳見解析.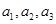 的表達式,可以歸納出數列
的表達式,可以歸納出數列 的通項公式為
的通項公式為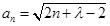 ,證明
,證明 不可能為等比數列可以考慮采用反證法來證明,假設
不可能為等比數列可以考慮采用反證法來證明,假設 為等比數列,可以得到與事實不符的等式,從而得證;(2)若
為等比數列,可以得到與事實不符的等式,從而得證;(2)若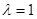 時,
時, 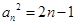 ∴
∴ ,
,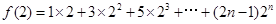 ,利用錯位相減法進行數列求和,即可得到f(2)的表達式;(3)當
,利用錯位相減法進行數列求和,即可得到f(2)的表達式;(3)當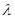 =4,欲證當
=4,欲證當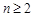 時,
時,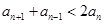 ,即證
,即證 ,嘗試采用分析法,從要證明的不等式出發,執果索因,即可得證
,嘗試采用分析法,從要證明的不等式出發,執果索因,即可得證 的通項公式為
的通項公式為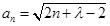 2分
2分 不可能為等比數列:
不可能為等比數列: 為等比數列,則
為等比數列,則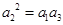 ,即
,即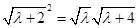 (
(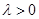 ),
),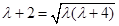 ,兩邊平方整理得:4=0,矛盾,
,兩邊平方整理得:4=0,矛盾, 不可能為等比數列 5分
不可能為等比數列 5分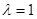 ,
,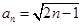 ,∴
,∴ 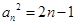 ,∴
,∴ ,
,
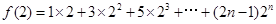 ①
①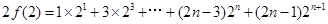 ②
②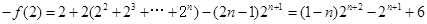
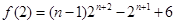 9分
9分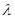 =4,
=4,
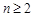 時,欲證
時,欲證 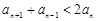 ,
,
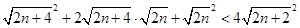
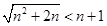
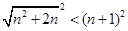

 成立,
成立,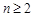 時,
時,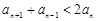 . 14分
. 14分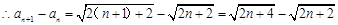
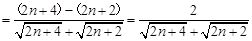

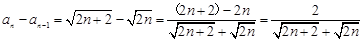
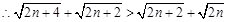 ,
,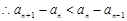 ,
,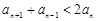 .
. 

 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源:不詳 題型:解答題
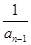 (n≥2,n∈N*).
(n≥2,n∈N*).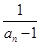 ,n∈N*,求證:數列{bn}是等差數列;
,n∈N*,求證:數列{bn}是等差數列;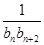 (n∈N*),求數列{cn}的前n項和Sn.
(n∈N*),求數列{cn}的前n項和Sn.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com