
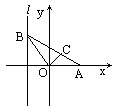
如圖,給出定點A(a,0)(a>0)和直線l:x=-1,B是直線l上的一動點,∠BOA的平分線交AB于點C,求點C的軌跡方程,并討論方程表示的曲線類型與a值的關系.(注:文科題設還有條件a≠1).
|
本題主要考查曲線與方程、直線和圓錐曲線等基礎知識以及求動點軌跡的基本技能和綜合運用數學知識解決問題的能力. 解:依題可設B(-1,b)(b∈R), ∴直線OB方程為y=-bx,設點C(x,y),則0≤x<a. ∵OC平分∠AOB, ∴點C到OA、OB距離相等. ∴|y|= 又直線AB的方程為y=- ∴b= y2[1+ 整理得y2[(1-a)x2-2ax+(1+a)y2]=0. 當y≠0時,(1-a)x2-2ax+(1+a)y2=0.(0<x<a) 當y=0時,b=0,∠AOB=π,C(0,0)滿足上式. ∴點C的軌跡方程為(1-a)x2-2ax+(1+a)y2=0(0≤x<a). ∵a≠1, ∴方程可化為 ∴當0<a<1時,此方程表示橢圓的一部分. 當a>1時,此方程表示雙曲線一支的一部分. |


科目:高中數學 來源: 題型:
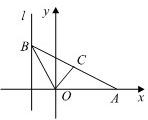 如圖,給出定點A(a,0)(a>0,a≠1)和直線l:x=-1,B是直線l上的動點,∠BOA的角平分線交AB于點C.求點C的軌跡方程,并討論方程表示的曲線類型與a值的關系.
如圖,給出定點A(a,0)(a>0,a≠1)和直線l:x=-1,B是直線l上的動點,∠BOA的角平分線交AB于點C.求點C的軌跡方程,并討論方程表示的曲線類型與a值的關系.查看答案和解析>>
科目:高中數學 來源: 題型:
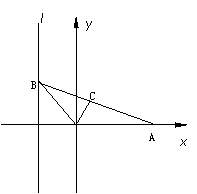
如圖,給出定點A(![]() , 0) (
, 0) (![]() >0)和直線: x = 1 . B是直線l上的動點,ÐBOA的角平分線交AB于點C. 求點C的軌跡方程,并討論方程表示的曲線類型與
>0)和直線: x = 1 . B是直線l上的動點,ÐBOA的角平分線交AB于點C. 求點C的軌跡方程,并討論方程表示的曲線類型與![]() 值的關系.(14分)
值的關系.(14分)
 |
查看答案和解析>>
科目:高中數學 來源: 題型:
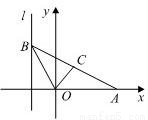
如圖,給出定點A(a,0) (a>0,a≠1)和直線l:x=-1,B是直線l上的動點,∠BOA的角平分線交AB于點C,求點C的軌跡方程,并討論方程表示的曲線類型與a值的關系.

查看答案和解析>>
科目:高中數學 來源:1999年全國統一高考數學試卷(文科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com