Question

(本題滿分14分)設有拋物線C：，通過原點O作C的切線，使切點P在第一象限.

   （1）求m的值，以及P的坐標；

   （2）過點P作切線的垂線，求它與拋物線的另一個交點Q；

   （3）設C上有一點R，其橫坐標為，為使DOPQ的面積小于DPQR的面積，試求的取值范圍.

Answer 1

（1）斜率k=，P的坐標為 （2，1）

（2）Q點的坐標為 （，－4）

（3）t的取值范圍為t<或t>.

解析:

設點P的坐標為（x₁， y₁），則y₁=kx₁……①，y₁= –+x₁ – 4……②，

         ①代入②，得：+（k–）x₁+4=0…………………………………………………2分

         因為點P為切點，所以 （k–）²–16=0，得：k=或k=……………………4分[來源:Z。xx。k.Com]

         當k=時x₁= －2，y₁= －17；當k=時，x₁= 2，y₁= 1；

         因為點P在第一象限，故所求的斜率k=，P的坐標為 （2，1），……………6分

法二：求導

   （2）過 P點作切線的垂線，其方程為：y=－2x+5……③，代入拋物線方程，得：

         x²－x+9=0，設Q點的坐標為 （x₂， y₂），則2x₂=9，所以x₂=，y₂=－4，

         所以Q點的坐標為 （，－4），………………………………………………10分

   （3）設C上有一點R（t，－t²+t–4），它到直線PQ的距離為：

         d==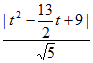……………………………………12分

         點O到直線PQ的距離PO =，S_DOPQ=??PQ??OP，S_DPQR=??PQ??d，

         因為DOPQ的面積小于DPQR的面積，S_DOPQ < S_DPQR ，

         即：OP < d，即：>5，……………………………………14分

         +4>0或+14<0

         解之得：t<或t>[來源:Zxxk.Com]

         所以t的取值范圍為t<或t>.……………………………16分

法二：做平行線