
f(x)=![]() ax3+bx2+cx+d,其中a、b、c、是以d為公差的等差數列,且a>0,d>0,設x0為f(x)的極小值點。在[1-
ax3+bx2+cx+d,其中a、b、c、是以d為公差的等差數列,且a>0,d>0,設x0為f(x)的極小值點。在[1-![]() ,0]上,f /(x)在x1處取最大值,在x2處取最小值,記點A(x0 ,f(x0)),B(x1 ,f/(x1)),C(x2 ,f/(x2))。
,0]上,f /(x)在x1處取最大值,在x2處取最小值,記點A(x0 ,f(x0)),B(x1 ,f/(x1)),C(x2 ,f/(x2))。
(1)求x0的值;
(2)若△ABC有一條邊平行于x軸,且面積為2+![]() ,求a、d的值。
,求a、d的值。
解:(1)∵2b=a+c
f/(x)=ax2+2bx+c= ax2+(a+c)x+c=a(x+1)(x+![]() )
)
∵a>0,d>0,∴![]() >1,
>1,
令f/(x)=0,得:x1=-![]() ,x2=-1,x1<x2,
,x2=-1,x1<x2,
列表可知,x1為極小值點,x2為極大值點;∴x0=-1;
(2)f/(x)的圖象是開口向上,對稱軸為x=-![]() 的拋物線,-
的拋物線,-![]() <-1,
<-1,
由f/(x)在[1-![]() ,0]上的圖象可知:最大值為f/(0)=c,即x1=0,
,0]上的圖象可知:最大值為f/(0)=c,即x1=0,
f/(x)在[1-![]() ,0]上的最小值為f/(-
,0]上的最小值為f/(-![]() )=-
)=-![]() ,即x2=-
,即x2=-![]() ,
,
∴A(-1,-![]() ),B(0,c),C(-
),B(0,c),C(-![]() ,-
,-![]() )
)
∵△ABC的一邊平行于x軸,∴AC平行于x軸,
∴-![]() =-
=-![]() ∴a=
∴a=![]() d,
d,
b=(![]() +1)d,c=(
+1)d,c=(![]() +2)d,代入
+2)d,代入
S△=![]() |(
|(![]() -1)(C+
-1)(C+![]() )|=2+
)|=2+![]() 得:
得:
∴d=3,a=3![]() 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
 已知函數f(x)=ax3+b,其圖象在點P處的切線為l:y=4x-4,點P的橫坐標為2(如圖).求直線l、直線x=0、直線y=0以及f(x)的圖象在第一象限所圍成區域的面積.
已知函數f(x)=ax3+b,其圖象在點P處的切線為l:y=4x-4,點P的橫坐標為2(如圖).求直線l、直線x=0、直線y=0以及f(x)的圖象在第一象限所圍成區域的面積.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數f(x)=ax3+b,其圖象在點P處的切線為l:y=4x-4,點P的橫坐標為2(如圖).求直線l、直線x=0、直線y=0以及f(x)的圖象在第一象限所圍成區域的面積.
已知函數f(x)=ax3+b,其圖象在點P處的切線為l:y=4x-4,點P的橫坐標為2(如圖).求直線l、直線x=0、直線y=0以及f(x)的圖象在第一象限所圍成區域的面積.查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省臨沂市郯城一中高二(下)4月月考數學試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
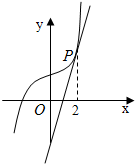
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com