
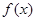 滿足
滿足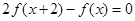 ,當
,當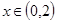 時,
時,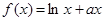
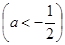 ,當
,當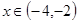 時,
時, 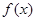 的最大值為-4.
的最大值為-4.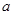 的值;
的值;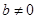 ,函數
,函數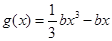 ,
,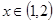 .若對任意的
.若對任意的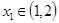 ,總存在
,總存在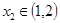 ,使
,使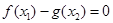 ,求實數
,求實數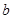 的取值范圍.
的取值范圍.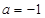 ; (II)
; (II)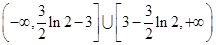
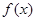 滿足
滿足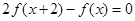 ,當
,當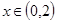 ,所以可得f(x)=2f(x+2)=4f(x+4)當x
,所以可得f(x)=2f(x+2)=4f(x+4)當x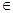 (-4,-2),則x+4
(-4,-2),則x+4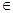 (0,2)這樣就可以f(x)=4f(x+4)=4ln(x+4)+4
(0,2)這樣就可以f(x)=4f(x+4)=4ln(x+4)+4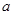 (x+4).所以通過求導可求出f(x)的導數,再根據
(x+4).所以通過求導可求出f(x)的導數,再根據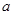 的取值范圍求出函數的單調區間即可求出最大值.從而解出
的取值范圍求出函數的單調區間即可求出最大值.從而解出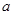 的值.
的值.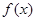 的值域為A,
的值域為A,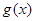 的值域為B,則由已知,對于任意的
的值域為B,則由已知,對于任意的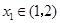
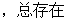
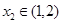 ,使
,使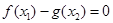 得,
得,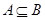 即函數f(x)值域的范圍比函數g(x)值域的范圍小即可.對于函數g(x)的單調性要考慮b的值.再根據,
即函數f(x)值域的范圍比函數g(x)值域的范圍小即可.對于函數g(x)的單調性要考慮b的值.再根據,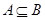 即可得結論.
即可得結論.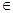 (0,2)時,f(x)=lnx+
(0,2)時,f(x)=lnx+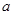 x.設x
x.設x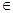 (-4,-2),則x+4
(-4,-2),則x+4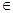 (0,2).所以f(x+4)="ln(x+4)+"
(0,2).所以f(x+4)="ln(x+4)+" 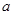 (x+4).所以x
(x+4).所以x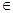 (-4,-2)時,f(x)=4f(x+4)=4ln(x+4)+4
(-4,-2)時,f(x)=4f(x+4)=4ln(x+4)+4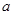 (x+4).所以
(x+4).所以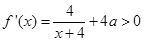 .因為x
.因為x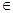 (-4,-2).所以
(-4,-2).所以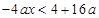 .因為
.因為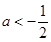 .所以
.所以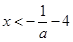 .又由
.又由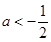 可得
可得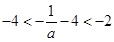 .所以f(x)在
.所以f(x)在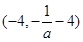 上是增函數,在
上是增函數,在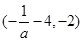 上是減函數.所以
上是減函數.所以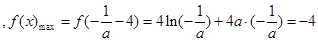 .所以
.所以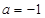 .
.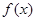 的值域為A,
的值域為A,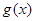 的值域為B,則由已知,對于任意的
的值域為B,則由已知,對于任意的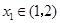
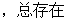
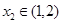 ,使
,使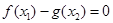 得,
得,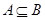 .
. 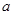 =-1,當
=-1,當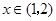 時,
時,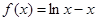 ,
,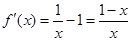 ,
,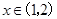 ,∴
,∴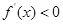 ,
,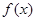 在
在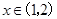 上單調遞減函數,
上單調遞減函數,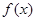 的值域為 A=
的值域為 A=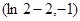
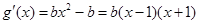 ,
,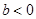 時,
時,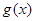 在
在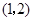 上是減函數,此時,
上是減函數,此時,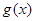 的值域為
的值域為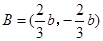 ,
,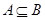 ,又
,又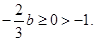 ∴
∴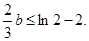 即
即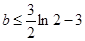 . 12分
. 12分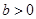 時,
時,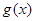 在
在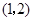 上是單調遞增函數,此時,
上是單調遞增函數,此時,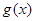 的值域為
的值域為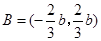 ,為滿足
,為滿足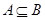 ,又,∴
,又,∴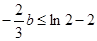 ,∴
,∴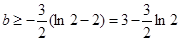 ,
,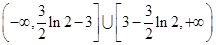 .
.

 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源:不詳 題型:解答題
 (單位:元,
(單位:元,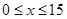 )的關系是t=
)的關系是t=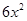 .
.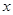 的函數;
的函數;查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
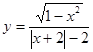 為奇函數;
為奇函數;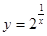 的值域是
的值域是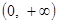 ;
;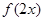 的定義域為
的定義域為 ,則函數
,則函數 的定義域為
的定義域為 ;
;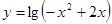 的單調遞增區間是
的單調遞增區間是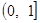 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com