
(08年福建卷理)(本小題滿分14分)
已知函數![]() .
.
(Ⅰ)求![]() 的單調區間;
的單調區間;
(Ⅱ)記![]() 在區間
在區間![]() (n∈N*)上的最小值為
(n∈N*)上的最小值為![]() ,令
,令![]() .
.
① 如果對一切n,不等式![]() 恒成立,求實數c的取值范圍;
恒成立,求實數c的取值范圍;
() 求證:![]() .
.
解析:解法一:
(I)因為![]() ,所以函數定義域為
,所以函數定義域為![]() ,且
,且![]() 。
。
由![]() 得
得![]() ,
,![]() 的單調遞增區間為
的單調遞增區間為![]() ;
;
由![]() <0得
<0得![]() ,
,![]() 的單調遞增區間為(0,+
的單調遞增區間為(0,+![]() ).
).
(Ⅱ)因為![]() 在
在![]() 上是減函數,所以
上是減函數,所以![]() ,
,
則![]() .
.
()![]()
![]()
又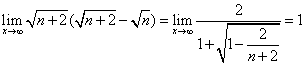 ,
,
因此![]() ,即實數c的取值范圍是
,即實數c的取值范圍是![]() .
.
() 由①知![]()
因為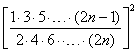
![]()
所以![]() <
<![]()
![]() ,
,
則![]()
![]()
![]() .
.
解法二:
(I)同解法一。
(Ⅱ)因為![]() 在
在![]() 上是減函數,所以
上是減函數,所以![]() ,
,
則![]() .
.
() 因為![]() 對
對![]() 恒成立,
恒成立,
所以![]() 對
對![]() 恒成立。
恒成立。
則![]() 對
對![]() 恒成立。
恒成立。
設![]() ,
,![]() ,則
,則![]() 對
對![]() 恒成立。
恒成立。
考慮![]() 。
。
因為![]()
![]() 在
在![]() 內是減函數;則當
內是減函數;則當![]() 時,
時,![]() 隨
隨![]() 的增大而減小。
的增大而減小。
又因為![]()
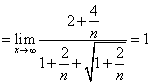 。
。
所以對一切![]() ,
,![]() 。因此
。因此![]() ,即實數c的取值范圍是
,即實數c的取值范圍是![]() .
.
() 由()知![]()
下面用數學歸納法證明不等式
![]()
![]() ,
,
① 當![]() 時,左邊
時,左邊![]() ,右邊
,右邊![]() ,左邊
,左邊![]() 右邊,不等式成立。
右邊,不等式成立。
② 假設當![]() 時,不等式成立.即
時,不等式成立.即![]() 。
。
當![]() 時,
時,
![]()
![]()
![]() 。
。
即![]() 時,不等式成立.
時,不等式成立.
綜合①、②得,![]()
![]() 成立。
成立。
所以![]()
![]()
![]()
![]() 。
。
![]() .
.
【高考考點】本小題主要考查函數的單調性、最值、不等式、數列等基本知識,考查運用導數研究函數性質的方法,考查分析問題和解決問題的能力,滿分14分.
【易錯提醒】第一問中導數記不住公式
【備考提示】此題為壓軸題,所以平時可以讓學生學會放棄一些自己能力范圍之外的題目,把多余的時間多花點在中低檔題目上,可是80%的分數呀,多么可觀,可是縱觀歷年的高考成績來看又有多少人真正的做到了這120分?


科目:高中數學 來源: 題型:
(08年福建卷理)(本小題滿分12分)
如圖,橢圓![]() 的一個焦點是
的一個焦點是![]() ,O為坐標原點.
,O為坐標原點.
(Ⅰ)已知橢圓短軸的兩個三等分點與一個焦點構成正三角
形,求橢圓的方程;
(Ⅱ)設過點F的直線l交橢圓于A、B兩點.若直線l繞點F
任意轉動,恒有![]() ,求a的取值范圍.
,求a的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
(08年福建卷理)(本小題滿分12分)
如圖,橢圓![]() 的一個焦點是
的一個焦點是![]() ,O為坐標原點.
,O為坐標原點.
(Ⅰ)已知橢圓短軸的兩個三等分點與一個焦點構成正三角
形,求橢圓的方程;
(Ⅱ)設過點F的直線l交橢圓于A、B兩點.若直線l繞點F
任意轉動,恒有![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年福建卷理)(本小題滿分12分)
某項考試按科目A、科目B依次進行,只有當科目A成績合格時,才可繼續參加科
目B的考試。已知每個科目只允許有一次補考機會,兩個科目成績均合格方可獲得證書。現某人參加這項考試,科目A每次考試成績合格的概率均為![]() ,科目B每次考試成績合格的概率均為
,科目B每次考試成績合格的概率均為![]() .假設各次考試成績合格與否均互不影響.
.假設各次考試成績合格與否均互不影響.
(Ⅰ)求他不需要補考就可獲得證書的概率;
(Ⅱ)在這項考試過程中,假設他不放棄所有的考試機會,記他參加考試的次數為![]() ,求
,求![]() 的數學期望E
的數學期望E![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年福建卷理)(本小題滿分12分)
已知函數![]() .
.
(Ⅰ)設![]() 是正數組成的數列,前n項和為
是正數組成的數列,前n項和為![]() ,其中
,其中![]() .若點
.若點![]() (n∈N*)在函數
(n∈N*)在函數![]() 的圖象上,求證:點
的圖象上,求證:點![]() 也在
也在![]() 的圖象上;
的圖象上;
(Ⅱ)求函數![]() 在區間
在區間![]() 內的極值.
內的極值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年福建卷理)(本小題滿分12分)
如圖,在四棱錐![]() 中,則面PAD⊥底面
中,則面PAD⊥底面![]() ,側棱
,側棱![]() ,底面
,底面![]() 為直角梯形,其中
為直角梯形,其中![]()
![]() ,
,![]() ,O為
,O為![]() 中點。
中點。
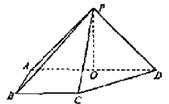
(Ⅰ)求證:PO⊥平面![]() ;
;
(Ⅱ)求異面直線PD與CD所成角的大小;
(Ⅲ)線段AD上是否存在點Q,使得它到平面PCD的距離為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com