
已知函數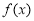 的定義域為
的定義域為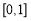 ,且
,且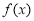 的圖象連續不間斷. 若函數
的圖象連續不間斷. 若函數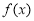 滿足:對于給定的
滿足:對于給定的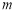 (
(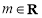 且
且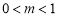 ),存在
),存在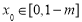 ,使得
,使得 ,則稱
,則稱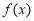 具有性質
具有性質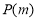 .
.
(1)已知函數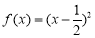 ,
,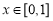 ,判斷
,判斷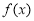 是否具有性質
是否具有性質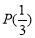 ,并說明理由;
,并說明理由;
(2)已知函數 若
若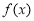 具有性質
具有性質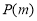 ,求
,求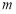 的最大值;
的最大值;
(3)若函數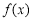 的定義域為
的定義域為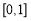 ,且
,且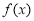 的圖象連續不間斷,又滿足
的圖象連續不間斷,又滿足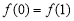 ,
,
求證:對任意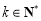 且
且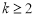 ,函數
,函數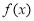 具有性質
具有性質 .
.
(1)具有該性質,證明見解析;(2)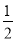 ;(3)證明見解析.
;(3)證明見解析.
【解析】
試題分析:(1)創新定義問題,首先要讀懂具有性質P(m)的意思, 對于給定的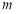 (
(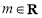 且
且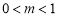 ),存在
),存在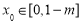 ,使得
,使得 ,按照此定義進行判斷,假設具有該性質, 設
,按照此定義進行判斷,假設具有該性質, 設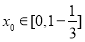 ,令
,令 ,解得
,解得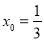
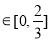 ,滿足定義,故具有性質P(3);(2)m在0到1之間,取一半,看是
,滿足定義,故具有性質P(3);(2)m在0到1之間,取一半,看是
具有性質P(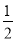 ),如果有,再判斷是否有大于
),如果有,再判斷是否有大于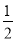 的m,沒有的話,最大值就是
的m,沒有的話,最大值就是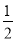 ;(3)構造函數
;(3)構造函數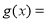
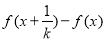 ,
, 則
則 ,
,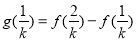 …
…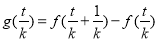 …
…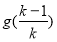 =
=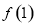 -
-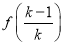 ,相加,有
,相加,有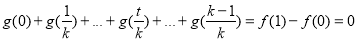 ,分里面有零和沒零進行討論,得到結論.
,分里面有零和沒零進行討論,得到結論.
試題解析:(1)設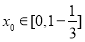 ,即
,即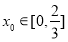
令 , 則
, 則
解得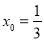
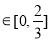 ,
,
所以函數 具有性質
具有性質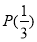
(2)m的最大值為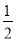 .
.
首先當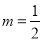 時,取
時,取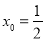 ,
,
則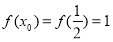 ,
,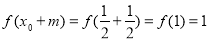 ,
,
所以函數 具有性質
具有性質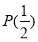 ,
,
假設存在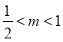 ,使得函數
,使得函數 具有性質
具有性質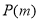 ,
,
則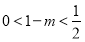 ,
,
當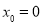 時,
時,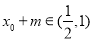 ,
,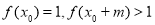 ,
,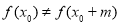 ,
,
當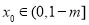 時,
時,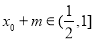 ,
,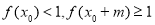 ,
,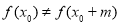 ,
,
所以不存在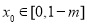 ,使得
,使得 ,
,
故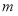 的最大值為
的最大值為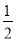 .
.
(3)任取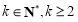 ,
,
設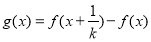 ,其中
,其中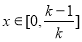 ,
,
 則有
則有 ,
,
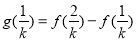 ,
,
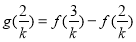 ,
,
……
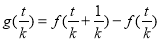 ,
,
……
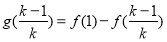 ,
,
以上各式相加得: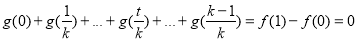 ,
,
當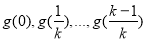 中有一個為
中有一個為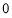 時,不妨設為
時,不妨設為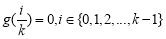 ,
,
即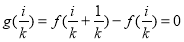 ,
,
則函數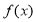 具有性質
具有性質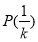 ,
,
當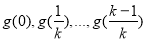 均不為
均不為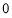 時,由于其和為
時,由于其和為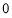 ,則必然存在正數和負數,
,則必然存在正數和負數,
不妨設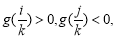 其中
其中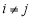 ,
,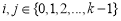 ,
,
由于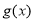 是連續的,所以當
是連續的,所以當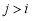 時,至少存在一個
時,至少存在一個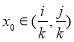 ,
,
(當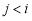 時,至少存在一個
時,至少存在一個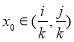 ),
),
使得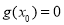 ,
,
即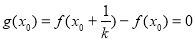 ,
,
故函數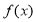 具有性質
具有性質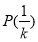 .
.
考點:1.抽象函數的定義;2.創新問題情境;3.構造函數.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:高中數學 來源:2016屆吉林白山市高一上學期期末考試數學卷(解析版) 題型:選擇題
定義在R上的函數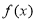 滿足:
滿足: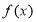 的圖像關于
的圖像關于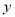 軸對稱,并且對任意的
軸對稱,并且對任意的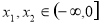
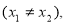 有
有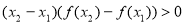 ,則當
,則當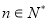 時,有( )
時,有( )
A.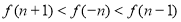 B.
B.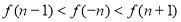
C.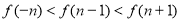 D.
D.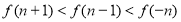
查看答案和解析>>
科目:高中數學 來源:2015屆重慶市高二上學期期末考試文科數學試卷(解析版) 題型:填空題
某大學對1000名學生的自主招生水平測試成績進行統計,得到樣本頻率分布直方圖如下圖所示,現規定不低于70分為合格,則合格人數是 _.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com