
如圖,在長方體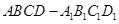 中,
中,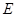 、
、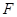 分別是棱
分別是棱 ,
,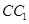
上的點,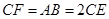 ,
,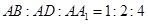
(1) 求異面直線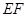 與
與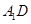 所成角的余弦值;
所成角的余弦值;
(2) 證明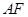
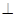 平面
平面
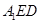
(3) 求二面角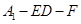 的正弦值。
的正弦值。
 ,
,
【解析】方法一:如圖所示,建立空間直角坐標系,
點A為坐標原點,設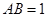 ,依題意得
,依題意得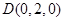 ,
,
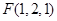 ,
,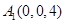 ,
,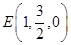
(1) 解:易得 ,
,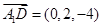
于是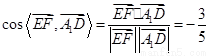
所以異面直線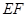 與
與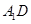 所成角的余弦值為
所成角的余弦值為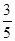
(2) 證明:已知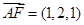 ,
,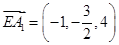 ,
,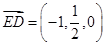
于是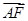 ·
·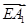 =0,
=0,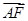 ·
·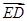 =0.因此,
=0.因此,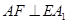 ,
,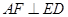 ,又
,又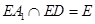
所以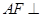 平面
平面
(3)解:設平面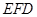 的法向量
的法向量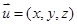 ,則
,則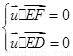 ,即
,即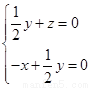
不妨令X=1,可得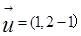 。由(2)可知,
。由(2)可知,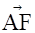 為平面
為平面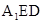 的一個法向量。
的一個法向量。
于是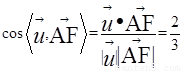 ,從而
,從而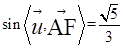
所以二面角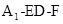 的正弦值為
的正弦值為
方法二:(1)解:設AB=1,可得AD=2,AA1=4,CF=1.CE=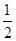
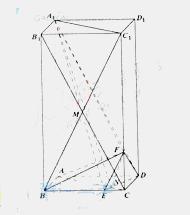 鏈接B1C,BC1,設B1C與BC1交于點M,易知A1D∥B1C,由
鏈接B1C,BC1,設B1C與BC1交于點M,易知A1D∥B1C,由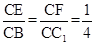 ,可知EF∥BC1.故
,可知EF∥BC1.故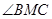 是異面直線EF與A1D所成的角,易知BM=CM=
是異面直線EF與A1D所成的角,易知BM=CM=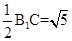 ,所以
,所以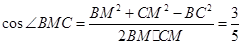 ,所以異面直線FE與A1D所成角的余弦值為
,所以異面直線FE與A1D所成角的余弦值為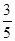
(2)證明:連接AC,設AC與DE交點N 因為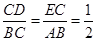 ,所以
,所以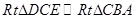 ,從而
,從而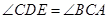 ,又由于
,又由于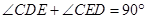 ,所以
,所以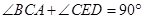 ,故AC⊥DE,又因為CC1⊥DE且
,故AC⊥DE,又因為CC1⊥DE且 ,所以DE⊥平面ACF,從而AF⊥DE.
,所以DE⊥平面ACF,從而AF⊥DE.
連接BF,同理可證B1C⊥平面ABF,從而AF⊥B1C,所以AF⊥A1D因為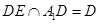 ,所以AF⊥平面A1ED
,所以AF⊥平面A1ED
(3)解:連接A1N.FN,由(2)可知DE⊥平面ACF,又NF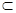 平面ACF, A1N
平面ACF, A1N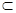 平面ACF,所以DE⊥NF,DE⊥A1N,故
平面ACF,所以DE⊥NF,DE⊥A1N,故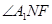 為二面角A1-ED-F的平面角
為二面角A1-ED-F的平面角
易知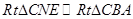 ,所以
,所以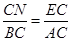 ,又
,又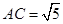 所以
所以 ,在
,在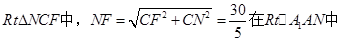
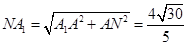
連接A1C1,A1F 在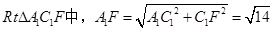
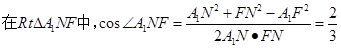 。所以
。所以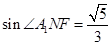
所以二面角A1-DE-F正弦值為


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
(08年惠州一中四模理) 如圖,在長方體![]() 中,
中,![]() ,點E在棱
,點E在棱![]() 上移動。
上移動。
(Ⅰ)證明:![]() ;
;
(Ⅱ)當E為![]() 的中點時,求點E到面
的中點時,求點E到面![]() 的距離;
的距離;
(Ⅲ)![]() 等于何值時,二面角
等于何值時,二面角![]() 的大小為
的大小為![]() 。
。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com