Question

（07年天津卷理）(14分)

設橢圓的左、右焦點分別為是橢圓上的一點原點到直線的距離為.

    (I)證明：；

    (II)設為橢圓上的兩個動點過原點作直線的垂線垂足為求點的軌跡方程.

Answer 1

解析：(I)證法一：由題設及不妨設點其中由于點在橢圓上，有即    解得從而得到

直線的方程為整理得

    由題設，原點到直線的距離為即

    將代入上式并化簡得即 

證法二：同證法一，得到點的坐標為

    過點作垂足為易知～故

   

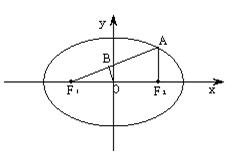
由橢圓定義得又所以

    解得而而得即

（II）解法一：設點的坐標為當時，由知，直線的斜率為

所以直線的方程為或其中

    點的坐標滿足方程組

    將①式代入②式，得

    整理得于是

     　　　　③

    由①式得  

                   　　　　④

    由知將③式和④式代入得

     將代入上式，整理得

    當時，直線的方程為點的坐標滿足方程組

     所以

    由知即解得

    這時，點的坐標仍滿足

    綜上，點的軌跡方程為

解法二：設點的坐標為直線的方程為由垂足為可知直線的方程為記（顯然點的坐標滿足方程組

                由①式得　　　　　　　③

    由②式得　　　④     將③式代入④式得

    整理得于是　　　　⑤

    由①式得   　　　　　　⑥

    由②式得   　　　　⑦

    將⑥式代入⑦式得

    整理得于是　　　　　⑧

    由知將⑤式和⑧式代入得

      將代入上式，得

    所以，點的軌跡方程為

【考點】本小題主要考查橢圓的標準方程和幾何性質、直線方程、求曲線的方程等基礎知識，考查曲線和方程的關系等解析幾何的基本思想方法及推理、運算能力.