
已知函數 ,其中
,其中 ,記函數
,記函數 的定義域為D.
的定義域為D.
(1)求函數 的定義域D;
的定義域D;
(2)若函數 的最小值為
的最小值為 ,求
,求 的值;
的值;
(3)若對于D內的任意實數 ,不等式
,不等式 <
< 恒成立,求實數
恒成立,求實數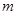 的取值范圍.
的取值范圍.
(1)
(2) 
(3) (-∞, )∪[
)∪[ ,+∞)
,+∞)
【解析】
試題分析:解:(1)要使函數有意義:則有 ,解得
,解得
∴ 函數的定義域D為 2分
2分
(2)


 ,
, ,即
,即 , 5分
, 5分
由 ,得
,得 ,
, .
7分
.
7分
(注: 不化簡為
不化簡為 扣1分)
扣1分)
(3)由題知-x2+2mx-m2+2m<1在x∈ 上恒成立,
上恒成立,
 -2mx+m2-2m+1>0在x∈
-2mx+m2-2m+1>0在x∈ 上恒成立, 8分
上恒成立, 8分
令g(x)=x2-2mx+m2-2m+1,x∈ ,
,
配方得g(x)=(x-m)2-2m+1,其對稱軸為x=m,
當m≤-3時, g(x)在 為增函數,
為增函數,
∴g(-3)= (-3-m)2-2m+1= m2+4m +10≥0,
而m2+4m +10≥0對任意實數m恒成立,∴m≤-3. 10分
②當-3<m<1時,函數g(x)在(-3,-1)為減函數,在(-1, 1)為增函數,
∴g(m)=-2m+1>0,解得m< ∴-3<m<
∴-3<m< 12分
12分
③當m≥1時,函數g(x)在 為減函數,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
為減函數,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
解得m≥ 或m≤
或m≤ , ∴-3<m<
, ∴-3<m< 14分
14分
綜上可得,實數m的取值范圍是 (-∞, )∪[
)∪[ ,+∞) 16分
,+∞) 16分
考點:函數的概念和值域,二次函數的最值
點評:解決的關鍵是利用函數的概念以及分離參數的思想來借助于二次函數的最值得到參數的范圍。屬于基礎題。


科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | an |
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年大連市雙基測試文)(14分)已知等差數列{an}滿足![]() ,設Sn是數列
,設Sn是數列![]() 的前n項和,
的前n項和,
記![]()
(1)求![]() ;
;
(2) 比較![]() 與
與![]() 其中
其中![]() 的大小;
的大小;
(3)如果函數![]() 對一切大于1的正整數n其函數值都小于零,那么a、b應滿足什么條件.
對一切大于1的正整數n其函數值都小于零,那么a、b應滿足什么條件.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2010年上海市金山區高考數學一模試卷(文理合卷)(解析版) 題型:解答題
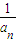 }的前n項和,記f(n)=S2n-Sn,
}的前n項和,記f(n)=S2n-Sn,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com