
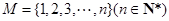 ,若集合
,若集合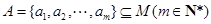 ,且對任意的
,且對任意的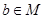 ,存在
,存在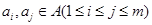 ,使得
,使得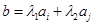 (其中
(其中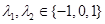 ),則稱集合
),則稱集合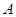 為集合
為集合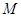 的一個
的一個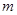 元基底.
元基底.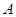 是否為集合
是否為集合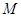 的一個二元基底,并說明理由;
的一個二元基底,并說明理由;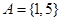 ,
,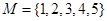 ;
;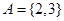 ,
,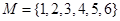 .
.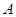 是集合
是集合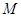 的一個
的一個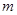 元基底,證明:
元基底,證明: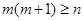 ;
;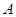 為集合
為集合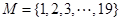 的一個
的一個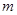 元基底,求出
元基底,求出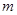 的最小可能值,并寫出當
的最小可能值,并寫出當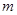 取最小值時
取最小值時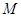 的一個基底
的一個基底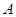 .
.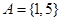 不是
不是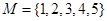 的一個二元基底.
的一個二元基底. ;
;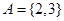 是
是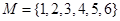 的一個二元基底.
的一個二元基底.  ,
, . 3分
. 3分 ,則
,則
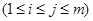 的正整數(shù)共有
的正整數(shù)共有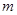 個;
個;
 的正整數(shù)共有
的正整數(shù)共有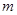 個;
個;
 的正整數(shù)至多有
的正整數(shù)至多有 個;
個;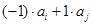
 的正整數(shù)至多有
的正整數(shù)至多有 個.
個. 含
含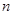 個不同的正整數(shù),
個不同的正整數(shù),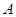 為集合
為集合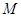 的一個
的一個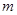 元基底.
元基底. ,即
,即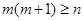 . 8分
. 8分 ,所以
,所以 .
. 時,
時, ,即用基底中元素表示出的數(shù)最多重復一個. *
,即用基底中元素表示出的數(shù)最多重復一個. * 為
為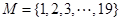 的一個4元基底,
的一個4元基底, ,則
,則 .
. 時,有
時,有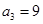 ,這時
,這時 或
或 .
. ,則由
,則由 ,與結論*矛盾.
,與結論*矛盾. ,則
,則 或
或 .易知
.易知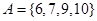 和
和 都不是
都不是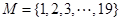 的4元基底,矛盾.
的4元基底,矛盾. 時,有
時,有 ,這時
,這時 ,
, ,易知
,易知 不是
不是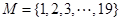 的4元基底,矛盾.
的4元基底,矛盾. 時,有
時,有 ,這時
,這時 ,
, ,易知
,易知 不是
不是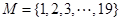 的4元基底,矛盾.
的4元基底,矛盾. 時,有
時,有 ,
, ,
, ,易知
,易知 不是
不是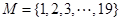 的4元基底,矛盾.
的4元基底,矛盾. 時,有
時,有 ,
, ,
, ,易知
,易知 不是
不是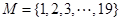 的4元基底,矛盾.
的4元基底,矛盾. 時,有
時,有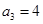 ,
, ,
, ,易知
,易知 不是
不是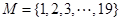 的4元基底,矛盾.
的4元基底,矛盾. 時,有
時,有 ,
, ,
,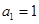 ,易知
,易知 不是
不是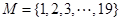 的4元基底,矛盾.
的4元基底,矛盾. 時,
時,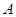 均不可能是
均不可能是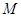 的4元基底.
的4元基底. 時,
時,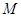 的一個基底
的一個基底 ;或{3,7,8,9,10};或{4,7,8,9,10}等,只要寫出一個即可.
;或{3,7,8,9,10};或{4,7,8,9,10}等,只要寫出一個即可.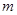 的最小可能值為5. 14分
的最小可能值為5. 14分

國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com