
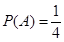 ;(Ⅱ)
;(Ⅱ)
 n
n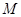 :(紅,紅),(紅,白1),(紅,白2),(紅,黑);(白1,紅)(白1,白1)(白1,白2),(白1,黑);(白2,紅),(白2,白1),(白2,白2),(白2,黑);(黑,紅),(黑,白1),(黑,白2),(黑,黑),所以
:(紅,紅),(紅,白1),(紅,白2),(紅,黑);(白1,紅)(白1,白1)(白1,白2),(白1,黑);(白2,紅),(白2,白1),(白2,白2),(白2,黑);(黑,紅),(黑,白1),(黑,白2),(黑,黑),所以 .…… 2分
.…… 2分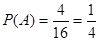 。 … 6分
。 … 6分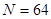 個; …………………………… 8分
個; …………………………… 8分 . ………………………… 12分
. ………………………… 12分

 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
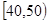 ,
,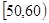 …
…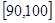 后畫出如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題:
后畫出如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題: ”的概率.
”的概率.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
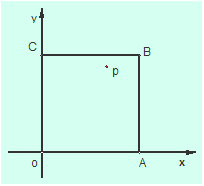
 處,準備開車到單位
處,準備開車到單位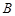 處上班,若該地各路段發生堵車事件都是相互獨立的,且在同一路段發生堵車事件最多只有一次,發生堵車事件的概率如圖(例如
處上班,若該地各路段發生堵車事件都是相互獨立的,且在同一路段發生堵車事件最多只有一次,發生堵車事件的概率如圖(例如 算作兩個路段:路段
算作兩個路段:路段 發生堵車事件的概率為
發生堵車事件的概率為 ,路段
,路段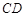 發生堵車事件的概率為
發生堵車事件的概率為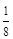 ).
).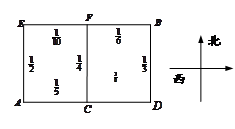
 到
到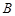 的最短路線(即此人只選擇從西向東和從南向北的路線),使得途中發生堵車事件的概率最小;
的最短路線(即此人只選擇從西向東和從南向北的路線),使得途中發生堵車事件的概率最小; 中遇到堵車次數為隨機變量
中遇到堵車次數為隨機變量 ,求
,求 的數學期望
的數學期望 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com