
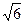 . (1)求證:AF//平面PCE;
. (1)求證:AF//平面PCE;
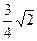 (3)
(3)
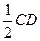
|
|
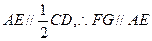 ∴四邊形AEGF是平行四邊形.
∴四邊形AEGF是平行四邊形. 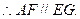
|
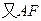
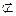 平面PCE,EG
平面PCE,EG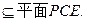
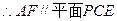 4分 (2)由(1)知點(diǎn)A到平面PCE的距離等于點(diǎn)F到
4分 (2)由(1)知點(diǎn)A到平面PCE的距離等于點(diǎn)F到
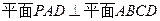
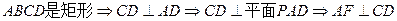
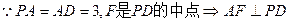
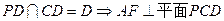

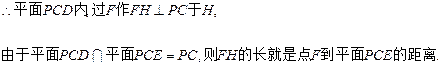
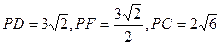 .
. .
. 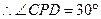 .
. 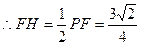 .
.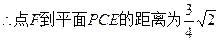 8分
8分 

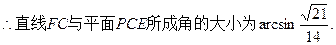 12分
12分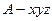 ,A(0,0,0),P(0,0,3),D(0,3,0),E(
,A(0,0,0),P(0,0,3),D(0,3,0),E( ,0,0),F(0,
,0,0),F(0,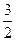 ,
,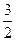 ),C(
),C(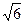 ,3,0) 2分
,3,0) 2分
|
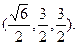
 ,
,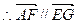
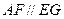 ,又
,又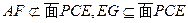
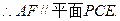 4分
4分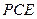 的法向量
的法向量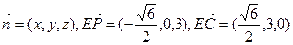 .
.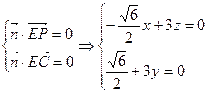 ,取
,取
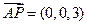 ,故
,故 到平面
到平面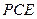 的距離為
的距離為 8分
8分 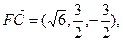
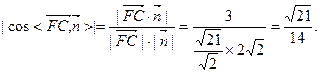
 直線FC與平面PCE所成角的大小為
直線FC與平面PCE所成角的大小為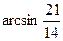 . 12分
. 12分


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 是邊長為6的正方形,
是邊長為6的正方形, ,
, ,
, ,點(diǎn)
,點(diǎn) 、
、 、
、 、
、 及
及 、
、 、
、 、
、 共線.(Ⅰ)沿圖中虛線將它們折疊起來,使
共線.(Ⅰ)沿圖中虛線將它們折疊起來,使 、
、 、
、 、
、 四點(diǎn)重合為點(diǎn)
四點(diǎn)重合為點(diǎn) ,請畫出其直觀圖;
,請畫出其直觀圖;

 的大小;(Ⅲ)試問需要幾個(gè)這樣的幾何體才能拼成一個(gè)棱長為6的正方體
的大小;(Ⅲ)試問需要幾個(gè)這樣的幾何體才能拼成一個(gè)棱長為6的正方體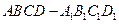 ?
?查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
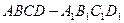 ,
,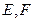 分別是
分別是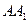 ,
,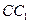 的中點(diǎn),P是
的中點(diǎn),P是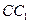 上的動點(diǎn)(包括端點(diǎn))過E、D、P作正方體的截面,若截面為四邊形,則P的軌跡是 ( )
上的動點(diǎn)(包括端點(diǎn))過E、D、P作正方體的截面,若截面為四邊形,則P的軌跡是 ( )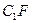 B、線段CF C、線段CF和點(diǎn)
B、線段CF C、線段CF和點(diǎn)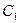 D、線段
D、線段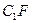 和一點(diǎn)C
和一點(diǎn)C查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
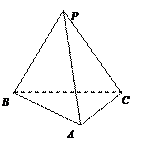
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 的底面
的底面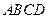 是半徑為
是半徑為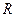 的圓的內(nèi)接四邊形,其中
的圓的內(nèi)接四邊形,其中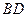 是圓的直徑,
是圓的直徑,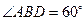 ,
,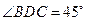 ,
,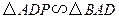 .
.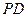 的長;
的長;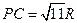 ,求三棱錐
,求三棱錐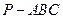 的體積.
的體積.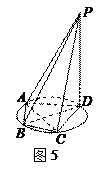
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.(1)是棱柱,(2)是棱臺 | B.(1)是棱臺,(2)是棱柱 |
| C.(1)(2)都是棱柱 | D.(1)(2)都是棱臺 |

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com