

 (
( 為常數),函數
為常數),函數 定義為:對每一個給定的實數
定義為:對每一個給定的實數 ,
,
 滿足條件
滿足條件 時,對于
時,對于 ,
, ;
; 是兩個實數,滿足
是兩個實數,滿足 ,且
,且 ,若
,若 ,求函數
,求函數 在區間
在區間 上的單調遞增區間的長度之和.(閉區間
上的單調遞增區間的長度之和.(閉區間 的長度定義為
的長度定義為 )
)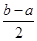
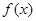 的解析式就是取
的解析式就是取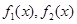 中較小的一個。所以
中較小的一個。所以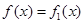 等價于
等價于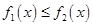 ,將此不等式轉化成指數函數不等式
,將此不等式轉化成指數函數不等式 ,根據指數的運算法則
,根據指數的運算法則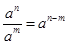 ,應將
,應將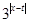 除過去用公式,再將不等式左邊的2也化為以3為底的對數,依據的公式是
除過去用公式,再將不等式左邊的2也化為以3為底的對數,依據的公式是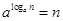 。再根據指數函數的單調性解同底的對數不等式。最后根據絕對值不等式的性質放縮不等式,即可求解。(2)根據(1)中所證已知
。再根據指數函數的單調性解同底的對數不等式。最后根據絕對值不等式的性質放縮不等式,即可求解。(2)根據(1)中所證已知 時,
時, ,圖形關于
,圖形關于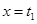 對稱,且在
對稱,且在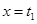 兩側單調性相反。若
兩側單調性相反。若 則
則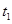 為
為 的中點。即可求得函數
的中點。即可求得函數 在區間
在區間 上的單調遞增區間的長度。當
上的單調遞增區間的長度。當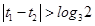 時,當
時,當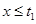 時
時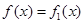 ,當
,當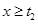 時
時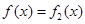 ,當
,當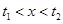 時解
時解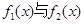 圖象交點的橫坐標,根據圖像得
圖象交點的橫坐標,根據圖像得 的解析式。再根據圖像得增區間,再求增區間的長度。
的解析式。再根據圖像得增區間,再求增區間的長度。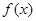 的定義可知,
的定義可知,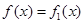 (對所有實數
(對所有實數 )等價于
)等價于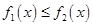 (對所有實數
(對所有實數 )這又等價于
)這又等價于 ,即
,即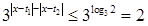 對所有實數
對所有實數 均成立. (*) 由于
均成立. (*) 由于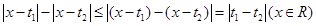 的最大值為
的最大值為 , 故(*)等價于
, 故(*)等價于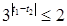 ,即
,即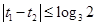 ,所以當
,所以當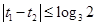 時,
時,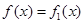
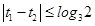 時,由(1)知
時,由(1)知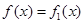 (對所有實數
(對所有實數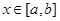 )
)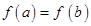 及
及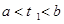 易知
易知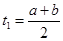 ,
,  的單調性可知,
的單調性可知,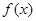 在區間
在區間 上的單調增區間的長度
上的單調增區間的長度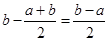 (參見示意圖1)
(參見示意圖1)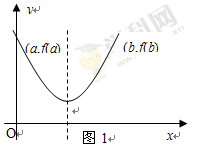
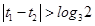 時,不妨設
時,不妨設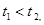 ,則
,則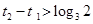 ,于是
,于是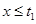 時,有
時,有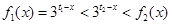 ,從而
,從而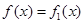 ;
;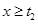 時,有
時,有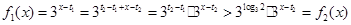
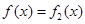 ;
;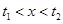 時,
時,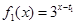 ,及
,及 ,由方程
,由方程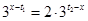
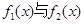 圖象交點的橫坐標為
圖象交點的橫坐標為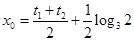 ⑴
⑴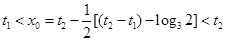 ,
,
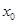 在
在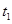 與
與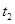 之間。由⑴易知
之間。由⑴易知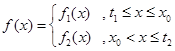
 上,
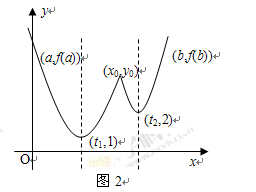
上,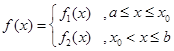 (參見示意圖2)
(參見示意圖2)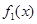 及
及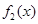 的單調性可知,
的單調性可知,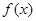 在區間
在區間 上的單調增區間的長度之和為
上的單調增區間的長度之和為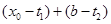 ,由于
,由于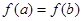 ,即
,即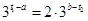 ,得
,得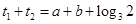 ⑵
⑵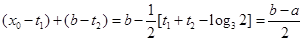
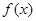 在區間
在區間 上的單調增區間的長度和為
上的單調增區間的長度和為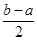 。
。

 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com