
在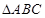 中,角
中,角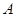 、
、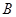 、
、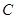 所對的邊分別為
所對的邊分別為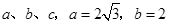 ,
,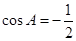 .
.
(1)求角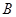 的大小;
的大小;
(2)若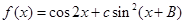 ,求函數
,求函數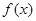 的最小正周期和單調遞增區間.
的最小正周期和單調遞增區間.
(1)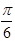 ;(2)
;(2)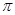 ,
,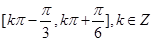 .
.
【解析】
試題分析:(1)解三角形問題先考慮運用正弦、余弦定理,此題先利用正弦定理可得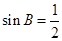 ,注意角A的余弦值為負值,即角A為鈍角,在三角形ABC中,角B只能為銳角,所以
,注意角A的余弦值為負值,即角A為鈍角,在三角形ABC中,角B只能為銳角,所以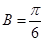 ;(2)再利用正弦定理易得
;(2)再利用正弦定理易得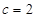 ,從而利用二倍角公式化簡函數
,從而利用二倍角公式化簡函數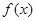 為一個角的三角函數式,易得函數
為一個角的三角函數式,易得函數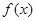 的周期,然后根據三角函數的性質求單調遞增區間(此處注意一定要寫成區間,并標明其中
的周期,然后根據三角函數的性質求單調遞增區間(此處注意一定要寫成區間,并標明其中 ).
).
試題解析:(1) ,
2分
,
2分
由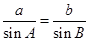 ,得
,得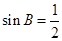 ,又A為鈍角,故B為銳角,
,又A為鈍角,故B為銳角,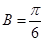 .(沒指出B范圍扣1分) 5分
.(沒指出B范圍扣1分) 5分
(2) 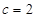 ,
7分
,
7分

 ,
9分
,
9分
所以,所求函數的最小正周期為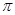 ,
,
由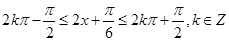 ,得
,得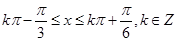 ,
,
所以所求函數的單調遞增區間為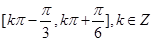 .(沒寫區間及指出K為整數扣1分) 12分
.(沒寫區間及指出K為整數扣1分) 12分
考點:1、正弦定理;2、二倍角公式;3、三角函數的單調區間.


科目:高中數學 來源:2010年湖北省高三第三次模擬考試(理科)數學卷 題型:解答題
(本小題滿分12分)(注意:在試題卷上作答無效)
在△ 中,角
中,角 、
、 、
、 所對的邊分別為
所對的邊分別為 、
、 、
、 ,且
,且 .
.
(Ⅰ)若 ,求角
,求角 ;
;
(Ⅱ)設 ,
,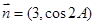 ,試求
,試求 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com