Question

(1)設a＞0,b＞0,c＞0且a+b+c=1,求證:8abc≤(1-a)(1-b)(1-c).

(2)設a,b,c為一個不等邊三角形的三邊,求證:abc＞(b+c-a)(a+b-c)(c+a-b).

(3)已知a＞0,b＞0,a+b=1,求證:(1+)(1+)≥25.

(4)設x＞0,y＞0,求證:.

Answer 1

證明：(1)∵a＞0,b＞0,c＞0且a+b+c=1,

∴1-a=b+c＞0.

同理,1-b=a+c＞0,1-c=a+b＞0,

∴(1-a)(1-b)(1-c)=(a+b)(b+c)(a+c).∵a+b≥2＞0,b+c≥2＞0,a+c≥2＞0,

∴(a+b)(b+c)(a+c)≥2·2·2=8abc(當a=b=c=時,等號成立).

(2)∵a,b,c為一個不等邊三角形的三邊,

∴a＞0,b＞0,c＞0且a+b-c＞0,a+c-b＞0,b+c-a＞0.

∵a=≥＞0,

同理,b=≥＞0,

c=＞0,

由于三角形是不等邊三角形,上述三式不能同時取“＝”,

∴abc＞(a+b-c)(b+c-a)(c+a-b).

(3)設y===

∵a＞0,b＞0,a+b=1,

∴a²+2ab+b²=1.

∴a²+b²=1-2ab.

∴y=1+令t=,則y=2t²-2t+1.

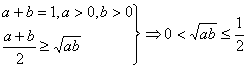,即0＜ab≤.

∴≥4,即t∈［4,+∞).

由二次函數(shù)的性質(zhì)可知對稱軸t=.

y=2t²-2t+1在t∈［4,+∞)上是增函數(shù).

∴當t=4時,y取最小值25.故(1+)(1+)≥25.

(4)∵x＞0,y＞0,∴(x²+y²)³=x⁶+y⁶+3x²y²(x²+y²)≥x⁶+y⁶+6x³y³＞x⁶+y⁶+2x³y³=(x³+y³)².

由不等式的性質(zhì),兩邊同時開6次方,得.