
(2006
湖南,18)如下圖,已知兩個正四棱錐P-ABCD與Q-ABCD的高分別為1和2,AB=4.(1)
證明:PQ⊥平面ABCD;(2)
求異面直線AQ與PB所成的角;(3)
求點P到平面QAD的距離.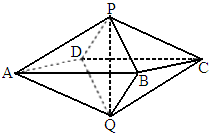
|
解析: (1)連結AC、BD,設AC∩BD=O,因為P-ABCD與Q-ABCD都是正四棱錐,所以PO⊥平面ABCD,QO⊥平面AB-CD,從而P、O、Q三點在一條直線上,所以PQ⊥平面ABCD.(2) 由題設知,ABCD是正方形,所以AC⊥BD.由 (1)知,PQ⊥平面ABCD,故可分別以直線CA、DB、QP為x軸、y軸、z軸建立空間直角坐標系(如圖),由題設條件,相關各點的坐標分別是P(0,0,1),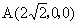 ,Q(0,0,-2), ,Q(0,0,-2), . .
所以  , ,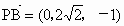 . .
于是 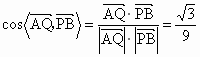 . .
從而異面直線 AQ與PB所成的角是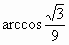 . .
(3) 由(2)知,點D的坐標是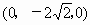 , ,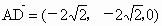 , ,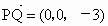 , ,
設 n=(x,y,z)是平面QAD的一個法向量,由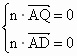 得 得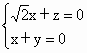 . .
取 x=1,得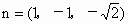 . .
所以點 P到平面QAD的距離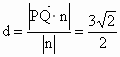 . . |


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com