
(08年北京卷理)(本小題共14分)
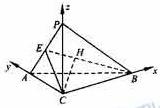
如圖,在三棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
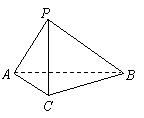
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求點![]() 到平面
到平面![]() 的距離.
的距離.
【標準答案】: 解法一:
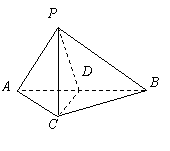
(Ⅰ)取![]() 中點
中點![]() ,連結
,連結![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
, ![]() .
.
(Ⅱ)![]() ,
,![]() ,
,
![]() .
.
又![]() ,
, ![]() .
.
又![]() ,即
,即![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中點
中點![]() .連結
.連結![]() .
.
![]() ,
,![]() .
.
![]() 是
是![]() 在平面
在平面![]() 內的射影,
內的射影,
![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 二面角
二面角![]() 的大小為
的大小為![]() .
.
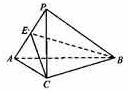
(Ⅲ)由(Ⅰ)知![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
過![]() 作
作![]() ,垂足為
,垂足為![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 的長即為點
的長即為點![]() 到平面
到平面![]() 的距離.
的距離.
由(Ⅰ)知![]() ,又
,又![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
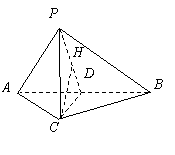
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() 點
點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
解法二:
(Ⅰ)![]() ,
,![]() ,
, ![]() .
.
又![]() ,
, ![]() .
.
![]() ,
, ![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)如圖,
以![]() 為原點建立空間直角坐標系
為原點建立空間直角坐標系![]() .
.
則![]() .
.
設![]() .
.
![]() ,
,
![]() ,
,![]() .
.
取![]() 中點
中點![]() ,連結
,連結![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
,![]() ,
,![]() ,
,
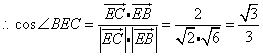 .
.
![]() 二面角
二面角![]() 的大小為
的大小為![]() .
.
(Ⅲ)![]() ,
,
![]() 在平面
在平面![]() 內的射影為正
內的射影為正![]() 的中心
的中心![]() ,且
,且![]() 的長為點
的長為點![]() 到平面
到平面![]() 的距離.
的距離.
如(Ⅱ)建立空間直角坐標系![]() .
.
![]() ,
, ![]() 點
點![]() 的坐標為
的坐標為![]() .
.
![]() .
.
![]() 點
點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
【高考考點】: 直線與直線的垂直,二面角,點面距離
【易錯提醒】: 二面角的平面角找不到,求點面距離的方法單一
【備考提示】: 找二面角的方法大致有十種左右,常見的也有五六種,希望能夠全面掌握。


科目:高中數學 來源: 題型:
(08年北京卷理)(本小題共14分)
已知菱形![]() 的頂點
的頂點![]() 在橢圓
在橢圓![]() 上,對角線
上,對角線![]() 所在直線的斜率為1.
所在直線的斜率為1.
(Ⅰ)當直線![]() 過點
過點![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(Ⅱ)當![]() 時,求菱形
時,求菱形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年北京卷理)(本小題共13分)
甲、乙等五名奧運志愿者被隨機地分到![]() 四個不同的崗位服務,每個崗位至少有一名志愿者.
四個不同的崗位服務,每個崗位至少有一名志愿者.
(Ⅰ)求甲、乙兩人同時參加![]() 崗位服務的概率;
崗位服務的概率;
(Ⅱ)求甲、乙兩人不在同一個崗位服務的概率。
(Ⅲ)設隨機變量![]() 為這五名志愿者中參加
為這五名志愿者中參加![]() 崗位服務的人數,求
崗位服務的人數,求![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com