
給出下列命題:
①半徑為2,圓心角的弧度數為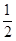 的扇形面積為
的扇形面積為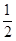 ;
;
②若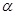 、
、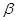 為銳角,
為銳角,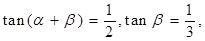 則
則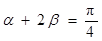 ;
;
③函數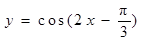 的一條對稱軸是
的一條對稱軸是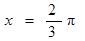 ;
;
④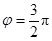 是函數
是函數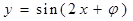 為偶函數的一個充分不必要條件.
為偶函數的一個充分不必要條件.
其中真命題的序號是 .
②③④
【解析】
試題分析:根據題意分別判定
①由扇形的面積公式可得S= ×22=1,則半徑為2,圓心角的弧度數為
×22=1,則半徑為2,圓心角的弧度數為 的扇形面積為1;故①錯誤
的扇形面積為1;故①錯誤
②由α、β為銳角,tan(α+β)= <1,tan β
<1,tan β <1,可得0<α+β<
<1,可得0<α+β< ,0<β<
,0<β< ,∴0<α+2β<
,∴0<α+2β<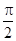 ,則tan(α+2β)=tan[(α+β)+β]=
,則tan(α+2β)=tan[(α+β)+β]=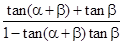 =1
=1
∴α+2β= ;故②正確③當x=
;故②正確③當x= 時,函數y=cos(2x-
時,函數y=cos(2x-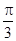 )=cosπ=-1取得函數的最小值,根據函數對稱軸處取得最值的性質可知,函數的一條對稱軸是x=
)=cosπ=-1取得函數的最小值,根據函數對稱軸處取得最值的性質可知,函數的一條對稱軸是x= ;③正確
;③正確
④∅=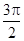 時,函數y=sin(2x+ϕ)=-cos2x為偶函數,但是當y=sin(2x+ϕ)為偶函數時,kπ+
時,函數y=sin(2x+ϕ)=-cos2x為偶函數,但是當y=sin(2x+ϕ)為偶函數時,kπ+ π=∅,即∅=
π=∅,即∅=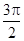 是函數y=sin(2x+ϕ)為偶函數時的一個充分不必要條件.④正確
是函數y=sin(2x+ϕ)為偶函數時的一個充分不必要條件.④正確
故答案為:②③④
考點:本試題主要以命題的真假關系的判斷為載體,主要考查了扇形的面積公式、兩角和的正切公式、正弦函數與余弦函數的對稱性質等知識的綜合應用,此類試題綜合性強,考查的知識點較多.
點評:解決該試題的關鍵對于三角函數性質的熟練運用。


科目:高中數學 來源: 題型:
| x2 |
| 4-t |
| y2 |
| t-1 |
| 5 |
| 2 |
| 5-2t |
| 1-t |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
查看答案和解析>>
科目:高中數學 來源:上海市十校2012屆高三第二次聯考數學文科試題 題型:022
下圖展示了一個區間(0,k)(k是一個給定的正實數)到實數集R的對應過程:區間(0,k)中的實數m對應線段AB上的點M,如圖1;將線段AB彎成半圓弧,圓心為H,如圖2;再將這個半圓置于直角坐標系中,使得圓心H坐標為(0,1),直徑AB平行x軸,如圖3;在圖形變化過程中,圖1中線段AM的長度對應于圖3中的圓弧AM的長度,直線HM與直線y=-1相交與點N(n,-1),則與實數m對應的實數就是n,記作n=f(m).給出下列命題:

(1)![]() ;
;
(2)函數n=f(m)是奇函數;
(3)n=f(m)是定義域上的單調遞增函數;
(4)n=f(m)的圖象關于點![]() 對稱;
對稱;
(5)方程f(m)=2的解是![]() .
.
其中正確命題序號為________.
查看答案和解析>>
科目:高中數學 來源:上海市十校2012屆高三第二次聯考數學理科試題 題型:022
下圖展示了一個區間(0,k)(k是一個給定的正實數)到實數集R的對應過程:區間(0,k)中的實數m對應線段AB上的點M,如圖1;將線段AB彎成半圓弧,圓心為H,如圖2;再將這個半圓置于直角坐標系中,使得圓心H坐標為(0,1),直徑AB平行x軸,如圖3;在圖形變化過程中,圖1中線段AM的長度對應于圖3中的圓弧AM的長度,直線HM與直線y=-1相交與點N(n,-1),則與實數m對應的實數就是n,記作n=f(m).給出下列命題:

(1)![]() ;(2)函數n=f(m)是奇函數;(3)n=f(m)是定義域上的單調遞增函數;(4)n=f(m)的圖象關于點
;(2)函數n=f(m)是奇函數;(3)n=f(m)是定義域上的單調遞增函數;(4)n=f(m)的圖象關于點![]() 對稱;(5)方程f(m)=2的解是
對稱;(5)方程f(m)=2的解是![]() .
.
其中正確命題序號為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com