
已知函數(shù)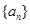 是首項(xiàng)為2,公比為
是首項(xiàng)為2,公比為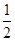 的等比數(shù)列,數(shù)列
的等比數(shù)列,數(shù)列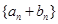 是首項(xiàng)為-2,第三項(xiàng)為2的等差數(shù)列.
是首項(xiàng)為-2,第三項(xiàng)為2的等差數(shù)列.
(1)求數(shù)列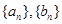 的通項(xiàng)式.
的通項(xiàng)式.
(2)求數(shù)列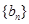 的前
的前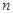 項(xiàng)和
項(xiàng)和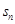 .
.
(1)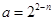 ,bn=2n-4-
,bn=2n-4-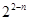 ; (2)Tn=n2-3n-4+
; (2)Tn=n2-3n-4+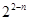 .
.
解析試題分析:(1)直接用等比數(shù)列等差數(shù)列即可求得數(shù)列{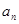 }{bn}的通項(xiàng)公式.
}{bn}的通項(xiàng)公式.
(2)數(shù)列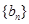 是一個(gè)等差數(shù)列與一個(gè)等比數(shù)列的和,故其求和采用分組求和的方法.
是一個(gè)等差數(shù)列與一個(gè)等比數(shù)列的和,故其求和采用分組求和的方法.
試題解析:(1)∵數(shù)列{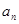 }是首項(xiàng)
}是首項(xiàng)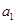 =2,公比q=
=2,公比q=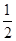 的等比數(shù)列,
的等比數(shù)列,
∴an=2·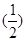 n-1=22-n,
n-1=22-n,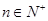 3分
3分
依題意得數(shù)列{bn+an}的公差d=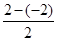 =2,
=2,
∴bn+an=-2+2(n-1)=2n-4,
∴bn=2n-4-22-n,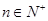 6分
6分
(2)設(shè)Sn為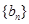 的前n項(xiàng)和,由(1)得 Sn=
的前n項(xiàng)和,由(1)得 Sn=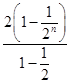 =4
=4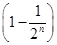 9分
9分
設(shè)數(shù)列{bn+an}的前n項(xiàng)和為Pn 則 Pn=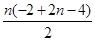 =n(n-3),
=n(n-3),
∴Tn=Pn-Sn=n(n-3)-4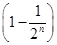 =n2-3n-4+22-n 12分
=n2-3n-4+22-n 12分
考點(diǎn):等差數(shù)列等比數(shù)列的通項(xiàng)公式及前n項(xiàng)和公式



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知正項(xiàng)數(shù)列{an}中,a1=1,且log3an,log3an+1是方程x2 (2n
(2n 1)x+bn=0的兩個(gè)實(shí)根.
1)x+bn=0的兩個(gè)實(shí)根.
(1)求a2,b1;
(2)求數(shù)列{an}的通項(xiàng)公式;
(3)若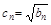 ,
,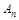 是
是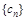 前
前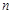 項(xiàng)和,
項(xiàng)和, 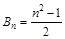 ,當(dāng)
,當(dāng) 時(shí),試比較
時(shí),試比較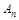 與
與 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知數(shù)列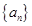 的各項(xiàng)都是正數(shù),且對(duì)任意
的各項(xiàng)都是正數(shù),且對(duì)任意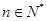 都有
都有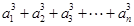
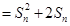 ,其中
,其中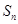 為數(shù)列
為數(shù)列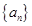 的前
的前 項(xiàng)和.
項(xiàng)和.
(1)求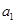 、
、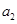 ;
;
(2)求數(shù)列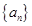 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)設(shè)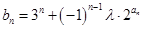 ,對(duì)任意的
,對(duì)任意的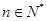 ,都有
,都有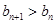 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)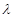 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分14分)已知數(shù)列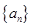 是各項(xiàng)均不為
是各項(xiàng)均不為 的等差數(shù)列,公差為
的等差數(shù)列,公差為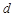 ,
, 為其前
為其前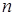 項(xiàng)和,且滿足
項(xiàng)和,且滿足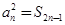 ,
,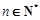 .?dāng)?shù)列
.?dāng)?shù)列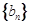 滿足
滿足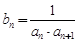 ,
,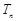 為數(shù)列
為數(shù)列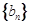 的前
的前 項(xiàng)和.
項(xiàng)和.
(1)求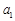 、
、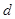 和
和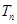 ;
;
(2)若對(duì)任意的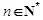 ,不等式
,不等式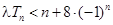 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)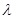 的取值范圍;
的取值范圍;
(3)是否存在正整數(shù)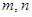
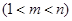 ,使得
,使得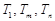 成等比數(shù)列?若存在,求出所有
成等比數(shù)列?若存在,求出所有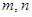 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
等差數(shù)列 中,
中,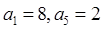 ,若在每相鄰兩項(xiàng)之間各插入一個(gè)數(shù),使之成為等差數(shù)列,
,若在每相鄰兩項(xiàng)之間各插入一個(gè)數(shù),使之成為等差數(shù)列,
那么新的等差數(shù)列的公差是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
已知在等差數(shù)列 中,
中, 的等差中項(xiàng)為
的等差中項(xiàng)為 ,
,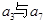 的等差中項(xiàng)為
的等差中項(xiàng)為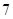 ,則數(shù)列
,則數(shù)列 的通項(xiàng)公式
的通項(xiàng)公式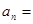 ( )
( )
A. | B. -1 -1 | C. +1 +1 | D. -3 -3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
已知等比數(shù)列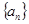 中,各項(xiàng)都是正數(shù),且
中,各項(xiàng)都是正數(shù),且 成等差數(shù)列,則
成等差數(shù)列,則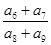 等于( )
等于( )
A.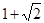 | B.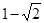 | C.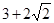 | D. |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
在數(shù)列 中,如果存在非零的常數(shù)
中,如果存在非零的常數(shù)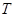 ,使
,使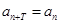 對(duì)于任意正整數(shù)
對(duì)于任意正整數(shù) 均成立,就稱數(shù)列
均成立,就稱數(shù)列 為周期數(shù)列,其中
為周期數(shù)列,其中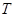 叫做數(shù)列
叫做數(shù)列 的周期. 已知數(shù)列
的周期. 已知數(shù)列 滿足
滿足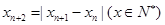 ,若
,若 ,當(dāng)數(shù)列
,當(dāng)數(shù)列 的周期為
的周期為 時(shí),則數(shù)列
時(shí),則數(shù)列 的前2012項(xiàng)的和為
的前2012項(xiàng)的和為
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com