
已知P為半圓C: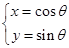 (
(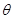 為參數(shù),
為參數(shù),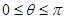 )上的點,點A的坐標為(1,0),
)上的點,點A的坐標為(1,0),
O為坐標原點,點M在射線OP上,線段OM與C的弧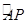 的長度均為
的長度均為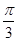 。
。
(Ⅰ)以O(shè)為極點, 軸的正半軸為極軸建立極坐標系,求點M的極坐標;
軸的正半軸為極軸建立極坐標系,求點M的極坐標;
(Ⅱ)求直線AM的參數(shù)方程。
(Ⅰ)由已知,M點的極角為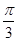 ,且M點的極徑等于
,且M點的極徑等于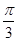 ,
,
故點M的極坐標為(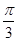 ,
,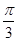 ). ……5分
). ……5分
(Ⅱ)M點的直角坐標為(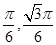 ),A(0,1),故直線AM的參數(shù)方程為
),A(0,1),故直線AM的參數(shù)方程為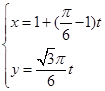 (t為參數(shù)) ……10分
(t為參數(shù)) ……10分
解析試題分析:(Ⅰ)由已知,M點的極角為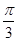 ,且M點的極徑等于
,且M點的極徑等于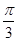 ,
,
故點M的極坐標為(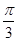 ,
,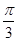 ). ……5分
). ……5分
(Ⅱ)M點的直角坐標為(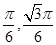 ),A(0,1),故直線AM的參數(shù)方程為
),A(0,1),故直線AM的參數(shù)方程為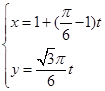 (t為參數(shù)) ……10分
(t為參數(shù)) ……10分
考點:本題主要考查直角坐標與極坐標的互化,直線的參數(shù)方程。
點評:簡單題,參數(shù)方程的給出,使解決問題的方法和思路得到擴充,有時利用曲線的參數(shù)方程,通過換元,可使問題較方便得解。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
已知圓 的極坐標方程是
的極坐標方程是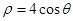 ,以極點為平面直角坐標系的原點,極軸為
,以極點為平面直角坐標系的原點,極軸為 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線 的參數(shù)方程是
的參數(shù)方程是 (
( 是參數(shù)).若直線
是參數(shù)).若直線 與圓
與圓 相切,求實數(shù)
相切,求實數(shù) 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在平面直角坐標系中,以坐標原點為極點,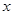 軸的非負半軸為極軸建立坐標系.已知點
軸的非負半軸為極軸建立坐標系.已知點 的極坐標為
的極坐標為 ,直線的極坐標方程為
,直線的極坐標方程為 ,且點
,且點 在直線上.
在直線上.
(1)求 的值及直線的直角坐標方程;
的值及直線的直角坐標方程;
(2)圓c的參數(shù)方程為 ,(
,( 為參數(shù)),試判斷直線與圓的位置關(guān)系.
為參數(shù)),試判斷直線與圓的位置關(guān)系.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)選修4-4:坐標系與參數(shù)方程
已知曲線C的極坐標方程是 .以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線l的參數(shù)方程是:
.以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線l的參數(shù)方程是: (
( 是參數(shù)).
是參數(shù)).
(I)將曲線C的極坐標方程和直線 參數(shù)方程轉(zhuǎn)化為普通方程;
參數(shù)方程轉(zhuǎn)化為普通方程;
(II)若直線l與曲線C相交于A、B兩點,且 ,試求實數(shù)
,試求實數(shù) 值.
值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在平面直角坐標系 中,已知曲線
中,已知曲線 ,以平面直角坐標系
,以平面直角坐標系 的原點
的原點 為極點,
為極點, 軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線
軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線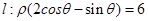 .
.
(1)將曲線 上的所有點的橫坐標、縱坐標分別伸長為原來的
上的所有點的橫坐標、縱坐標分別伸長為原來的 、
、 倍后得到曲線
倍后得到曲線 ,試寫出直線的直角坐標方程和曲線
,試寫出直線的直角坐標方程和曲線 的參數(shù)方程;
的參數(shù)方程;
(2)在曲線 上求一點
上求一點 ,使點
,使點 到直線的距離最大,并求出此最大值
到直線的距離最大,并求出此最大值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
如圖是某賽季甲、乙兩名籃球運動員每場比賽得分的莖葉圖,則甲、乙兩人這幾場比賽得分的中位數(shù)之和是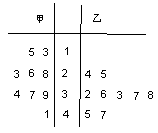
| A.62 | B.63 | C.64 | D.65 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
工人工資(元)依勞動生產(chǎn)率(千元)變化的回歸方程為y=50+80x,下列判斷中正確的是( )
| A.勞動生產(chǎn)率為1000元時,工資為130元 |
| B.勞動生產(chǎn)率平均提高1000元時,工資平均提高80元 |
| C.勞動生產(chǎn)率平均提高1000元時,工資平均提高130元 |
| D.當工資為250元時,勞動生產(chǎn)率為2000元 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com