
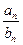 ,求數列{cn}的前n項和Tn.
,求數列{cn}的前n項和Tn. ,所以q=
,所以q= ,
, ,即bn=
,即bn= . …………………………6分
. …………………………6分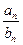 =
= =(2n-1) 4n-1, …………………………8分
=(2n-1) 4n-1, …………………………8分 -(2n-1)4n
-(2n-1)4n
 [(6n-5)4n+5].
[(6n-5)4n+5].

科目:高中數學 來源:不詳 題型:解答題
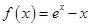 (
(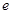 是自然對數的底數)
是自然對數的底數)
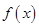 的最小值;
的最小值;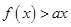 的解集為P, 若
的解集為P, 若
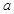 的取值范圍;
的取值范圍;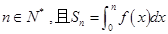 ,是否存在等差數列
,是否存在等差數列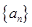 和首項為
和首項為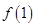 公比大于0的等比數列
公比大于0的等比數列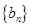 ,使數列
,使數列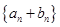 的前n項和等于
的前n項和等于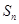
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 對任意的正整數n,都有
對任意的正整數n,都有 (d為常數),則稱
(d為常數),則稱 為“絕對和數列”,d叫做“絕對公和”,已知“絕對和數列”
為“絕對和數列”,d叫做“絕對公和”,已知“絕對和數列” ,“絕對公和”
,“絕對公和” ,則其前2010項和
,則其前2010項和 的最小值為
的最小值為 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com