
 的取值范圍;
的取值范圍;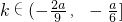 .
. >0,
>0,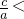 1.
1.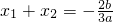 ,x1x2=
,x1x2=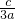 ,
, =
=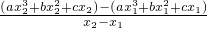
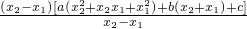
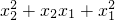 )+b(x2+x1)+c
)+b(x2+x1)+c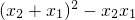 ]+b(x2+x1)+c
]+b(x2+x1)+c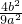 -
-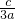 )+b(-
)+b(-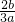 )+c
)+c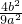 -
-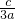 )+
)+ (-
(-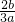 )+
)+ ]
]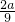 (-
(- +
+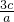 ),
), ,由b=-(a+c)得,
,由b=-(a+c)得, =-1-t,t∈(0,1),
=-1-t,t∈(0,1),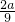 [-(1+t)2+3t]=
[-(1+t)2+3t]=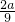 (-t2+t-1),
(-t2+t-1), ],∴k∈(-
],∴k∈(-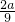 ,-
,- ].
]. 的二次不等式即可求得
的二次不等式即可求得 的取值范圍;
的取值范圍;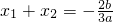 ,x1x2=
,x1x2=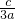 ,把韋達定理代入k=
,把韋達定理代入k= 可得關于a,b,c的表達式,令t=
可得關于a,b,c的表達式,令t= ,k可化為關于t的二次函數式,借助(1)問t的范圍即可求得k的范圍;
,k可化為關于t的二次函數式,借助(1)問t的范圍即可求得k的范圍;

 一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com