
在一個特定時段內,以點E為中心的7n mile以內海域被設為警戒水域.點E正北55n mile處有一個雷達觀測站A,某時刻測得一艘勻速直線行駛的船只位于點A北偏東45°且與點A相距40 n mile的位置B,經過40分鐘又測得該船已行駛到點A北偏東
n mile的位置B,經過40分鐘又測得該船已行駛到點A北偏東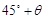 (其中
(其中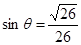 ,
,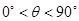 )且與點A相距10
)且與點A相距10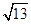 n mile的位置C.
n mile的位置C.
(I)求該船的行駛速度(單位:n mile /h);
(II)若該船不改變航行方向繼續行駛.判斷它是否會進入警戒水域,并說明理由.
(I)船的行駛速度為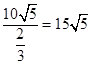 (海里/小時).(II)船會進入警戒水域.
(海里/小時).(II)船會進入警戒水域.
解析試題分析:(I)根據同角三角函數的基本關系式求出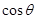 ,然后利用余弦定理求出BC的值,從而可求出船的行駛速度.
,然后利用余弦定理求出BC的值,從而可求出船的行駛速度.
(II)判斷船是否會進入警戒水域,關鍵是看點E到直線l的距離與半徑7的關系,因而可求出直線l的方程,以及E點坐標,然后再根據點到直線的距離公式得到結論.
(I)如圖,AB=40 ,AC=10
,AC=10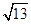 ,
,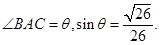
由于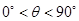 ,所以cos
,所以cos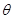 =
=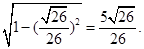
由余弦定理得BC=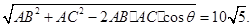
所以船的行駛速度為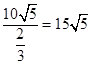 (海里/小時).
(海里/小時).
(II)解法一 如圖所示,以A為原點建立平面直角坐標系,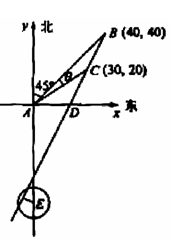
設點B、C的坐標分別是B(x1,y2), C(x1,y2),
BC與x軸的交點為D.
由題設有,x1=y1= 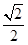 AB=40,
AB=40,
x2=ACcos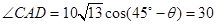 ,
,
y2=ACsin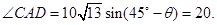
所以過點B、C的直線l的斜率k=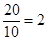 ,直線l的方程為y=2x-40.
,直線l的方程為y=2x-40.
又點E(0,-55)到直線l的距離d=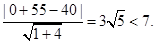
所以船會進入警戒水域.
解法二: 如圖所示,設直線AE與BC的延長線相交于點Q.
在△ABC中,由余弦定理得,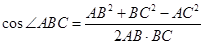 =
=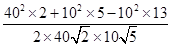 =
=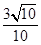 .
.
從而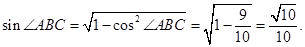
在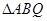 中,由正弦定理得,AQ=
中,由正弦定理得,AQ=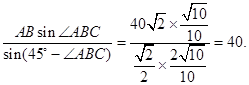
由于AE=55>40=AQ,所以點Q位于點A和點E之間,且QE=AE-AQ=15.
過點E作EP  BC于點P,則EP為點E到直線BC的距離.
BC于點P,則EP為點E到直線BC的距離.
在Rt 中,PE=QE·sin
中,PE=QE·sin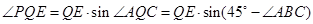
=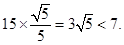 所以船會進入警戒水域.
所以船會進入警戒水域.
考點:正余弦定理在解三角形當中的應用,直線方程,點到直線的距離,直線與圓的位置關系.
點評:掌握正余弦定理及能解決的三角形類型是解三角形的前提.第(II)問關鍵是知道如何判斷船是否會進入警戒水域,實質是直線與圓的位置關系的判斷.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知在銳角△ABC中,a, b, c分別為角A、B、C所對的邊,向量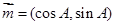 ,
,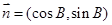 ,
,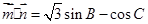 .
.
(1)求角A的大小;
(2)若a=3,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
在△ABC中,內角A、B、C所對邊的長分別為a、b、c,已知向量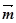 ="(1,cosA" -1),
="(1,cosA" -1),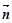 =(cosA,1)且滿足
=(cosA,1)且滿足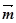 ⊥
⊥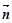 .
.
(Ⅰ)求A的大小;
(Ⅱ)若a= ,b+c=3 求b、c的值.
,b+c=3 求b、c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在某海濱城市附近海面有一臺風,據檢測,當前臺風中心位于城市O(如圖)的東偏南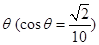 方向300 km的海面P處,并以20 km / h的速度向西偏北
方向300 km的海面P處,并以20 km / h的速度向西偏北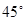 的方向移動,臺風侵襲的范圍為圓形區域,當前半徑為60 km ,并以10 km / h的速度不斷增加,問幾小時后該城市開始受到臺風的侵襲?持續多長時間?
的方向移動,臺風侵襲的范圍為圓形區域,當前半徑為60 km ,并以10 km / h的速度不斷增加,問幾小時后該城市開始受到臺風的侵襲?持續多長時間?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com