
如圖甲,已知PA垂直于⊙O所在平面,AB是⊙O的直徑,點C為圓周上異于A、B的一點.
(1)若一個 面體中有
面體中有 個面是直角三角形,則稱這個
個面是直角三角形,則稱這個 面體的直度為
面體的直度為 .那么四面體
.那么四面體 的直度為多少?說明理由;
的直度為多少?說明理由;
 (2)在四面體
(2)在四面體 中,
中, ,設
,設 .若動點
.若動點 在四面體
在四面體 表面上運動,并且總保持
表面上運動,并且總保持 .設
.設 為動點
為動點 的軌跡圍成的封閉圖形的面積關于角
的軌跡圍成的封閉圖形的面積關于角 的函數,求
的函數,求 取最大值時,二面角
取最大值時,二面角 的正切值.
的正切值.
解:(1)四面體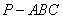 的直度為1.
的直度為1.
 理由如下:由AB是⊙O的直徑,點C為圓周上異于A、B的一點,故AC⊥BC, 從而底面為
理由如下:由AB是⊙O的直徑,點C為圓周上異于A、B的一點,故AC⊥BC, 從而底面為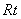 △。又PA垂直于⊙O所在平面,有PA⊥AB,PA⊥AC,故△PAB、△PAC都為
△。又PA垂直于⊙O所在平面,有PA⊥AB,PA⊥AC,故△PAB、△PAC都為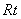 △。又AC為PC在面ABC內的射影,由三垂線定理知PC⊥BC,故△PCB為
△。又AC為PC在面ABC內的射影,由三垂線定理知PC⊥BC,故△PCB為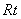 △。綜上知四面體
△。綜上知四面體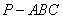 的四個面都為
的四個面都為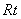 △,所以四面體
△,所以四面體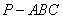 的直度為1. -----------------4分
的直度為1. -----------------4分
(2)∵動點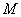 在四面體
在四面體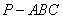 表面上運動,并且總保持
表面上運動,并且總保持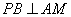 ,
,
∴動點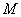 的軌跡是過點A作PB的垂面與四面體
的軌跡是過點A作PB的垂面與四面體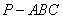 表面的交線圍成的三角形。
表面的交線圍成的三角形。
如圖乙:平面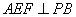 ,并且平面
,并且平面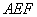 與四面體
與四面體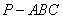 的三個側面分別交于AE、AF、EF.
的三個側面分別交于AE、AF、EF.
易知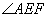 即為二面角
即為二面角 的平面角.
的平面角.
∵AB是⊙O的直徑,點C為圓周上異于A、B的一點,∴BC⊥AC
∵PA⊥面ABC,BC 平面ABC,∴BC⊥PA,故BC⊥面PAC,∵AF
平面ABC,∴BC⊥PA,故BC⊥面PAC,∵AF 平面PAC,∴AF⊥BC.
平面PAC,∴AF⊥BC.
又平面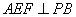 知AF⊥PB,∴AF⊥面PBC.又EF
知AF⊥PB,∴AF⊥面PBC.又EF 平面PBC,AF⊥FE,則
平面PBC,AF⊥FE,則 為
為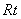 △.
△.
在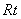 △PAB中,
△PAB中,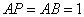 ,
, ,則AE=
,則AE=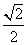 .
.
在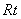 △ACB中,
△ACB中,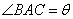 ,
, ,有
,有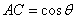 .
.
又在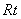 △PAC中,
△PAC中,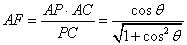 .
.
在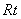
 中,
中,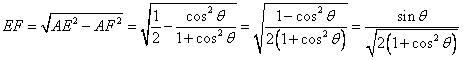 .
.
∴ =
=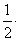


=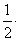

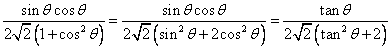

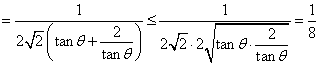 .
.
當且僅當 時
時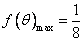 .
.
此時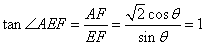 .
.
故 取最大值時二面角
取最大值時二面角 的正切值為1.------------12分
的正切值為1.------------12分


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com