甲、乙、丙三人分別獨立的進行某項技能測試，已知甲能通過測試的概率是
，甲、乙、丙三人都能通過測試的概率是
，甲、乙、丙三人都不能通過測試的概率是
，且乙通過測試的概率比丙大.
（Ⅰ）求乙、丙兩人各自通過測試的概率分別是多少；
（Ⅱ）求測試結束后通過的人數
的數學期望
.
百年學典課時學練測系列答案科目：高中數學 來源： 題型：解答題
（本小題滿分13分）把一個正方體的表面涂上紅色，在它的長、寬、高上等距離地各切三刀，則大正方體被分割成64個大小相等的小正方體，將這些小正方體均勻地攪混在一起，如果從中任取1個，求下列事件的概率
（1）事件A＝“這個小正方體各個面都沒有涂紅色”
（2）事件B＝“這個小正方體只有1個面涂紅色”
（3）事件C＝“這個小正方體至少2個面涂紅色”
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本大題9分）袋中有2個紅球，n個白球，各球除顏色外均相同.已知從袋中摸出2個球均為白球的概率為
，（Ⅰ）求n；（Ⅱ）從袋中不放回的依次摸出三個球，記ξ為相鄰兩次摸出的球不同色的次數（例如：若取出的球依次為紅球、白球、白球，則ξ=1），求隨機變量ξ的分布列及其數學期望Eξ.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）某高中為了推進新課程改革，滿足不同層次學生的需求，決定從高一年級開始，在每周的周一、周三、周五的課外活動期間同時開設數學、物理、化學、生物和信息技術輔導講座，每位有興趣的同學可以在期間的任何一天參加任何一門科目的輔導講座，也可以放棄任何一門科目的輔導講座。（規定：各科達到預先設定的人數時稱為滿座，否則稱為不滿座）統計數據表明，各學科講座各天的滿座的概率如下表：
根據上表：
（1）求數學輔導講座在周一、周三、周五都不滿座的概率；
（2）設周三各輔導講座滿座的科目數為
，求隨機變量的分布列和數學期望。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
為加強中學生實踐、創新能力和團隊精神的培養，促進教育教學改革，教育部門主辦了全國中學生航模競賽. 該競賽分為預賽和決賽兩個階段，參加決賽的隊伍按照抽簽方式決定出場順序.通過預賽，選拔出甲、乙、丙和丁四支隊伍參加決賽.
（Ⅰ）求決賽中甲、乙兩支隊伍恰好排在前兩位的概率；
⑾求決賽中甲、乙兩支隊伍出場順序相鄰的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分10分）一名學生在軍訓中練習射擊項目，他射擊一次，命中目標的概率是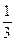
，若連續射擊6次，且各次射擊是否命中目標相互之間沒有影響．
（1）求這名學生在第3次射擊時，首次命中目標的概率；
（2）求這名學生在射擊過程中，恰好命中目標3次的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（14分）（理）袋中裝有黑球和白球共7個,從中任取2個球都是白球的概率為
現有甲、乙兩人從袋中輪流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到兩人中有一人取到白球時既終止，每個球在每一次被取出的機會是等可能的，用
表示取球終止所需要的取球次數．
（I）求袋中所有的白球的個數；
（II）求隨機變量的概率分布；
（III）求甲取到白球的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）一個盒子中裝有5張卡片，每張卡片上寫有一個數字，數字分別是1、2、3、4、5，現從盒子中隨機抽取卡片。
（1）從盒中依次抽取兩次卡片，每次抽取一張，取出的卡片不放回，求兩次取到的卡片的數字既不全是奇數，也不全是偶數的概率；
（2）若從盒子中有放回的抽取3次卡片，每次抽取一張，求恰有兩次取到卡片的數字為偶數的概率；
（3）從盒子中依次抽取卡片，每次抽取一張，取出的卡片不放回，當放回記有奇數的卡片即停止抽取，否則繼續抽取卡片，求抽取次數X的分布列和期望。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
設
為實數，我們稱
為有序實數對．類似地，設
為集合，我們稱
為有序三元組．如果集合滿足
，且
，則我們稱有序三元組為最小相交（
表示集合
中的元素的個數）．
（Ⅰ）請寫出一個最小相交的有序三元組，并說明理由；
（Ⅱ）由集合
的子集構成的所有有序三元組中，令
為最小相交的有序三元組的個數，求的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
、
依題意得：
即
或 
（舍去）┅┅┅┅┅┅┅4分
、
. ┅┅┅┅┅┅┅6分
