
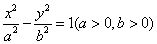 ��һ�l�u����������y=
��һ�l�u����������y=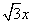 ,����һ��(g��)���c(di��n)�ڒ��タ
,����һ��(g��)���c(di��n)�ڒ��タ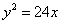 �Ĝ�(zh��n)���ϣ��t�p�����ķ��̞�
�Ĝ�(zh��n)���ϣ��t�p�����ķ��̞�A��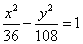 | B��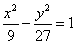  |
C��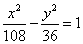 | D��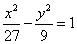 |
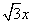 ����
���� �����a2=9��b2=27�������p�����ķ��̞�
�����a2=9��b2=27�������p�����ķ��̞�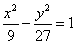 ���xB��
���xB��

 ���(zh��n)�п�����ϵ�д�
���(zh��n)�п�����ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
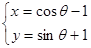 ����
���� �酢��(sh��)������ͨ���̞� �� ��
�酢��(sh��)������ͨ���̞� �� ��A��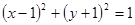 | B��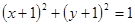 |
C��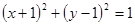 | D�� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
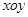 ��ԭ�c(di��n)���O�S��x�S�������S���ɷN����(bi��o)ϵ�е��L(zh��ng)�Ȇ�λ��ͬ����֪����
��ԭ�c(di��n)���O�S��x�S�������S���ɷN����(bi��o)ϵ�е��L(zh��ng)�Ȇ�λ��ͬ����֪����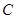 �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�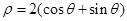 ��
��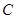 ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�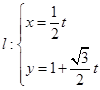 ��
��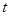 �酢��(sh��)���c����C����
�酢��(sh��)���c����C����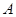 ��
��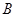 ���c(di��n)���c
���c(di��n)���c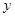 �S����
�S����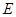 ����
����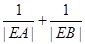 ��ֵ��
��ֵ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
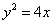 �Ľ��c(di��n)��F���c(di��n)
�Ľ��c(di��n)��F���c(di��n) ��ԓ���タ�ϵĄ�(d��ng)�c(di��n)�����c(di��n)
��ԓ���タ�ϵĄ�(d��ng)�c(di��n)�����c(di��n) �t
�t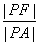 ����Сֵ��
����Сֵ��A��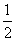 | B��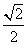 | C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
 �քe�ǙE�A��
�քe�ǙE�A�� ���ҽ��c(di��n)��
���ҽ��c(di��n)��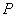 �ǵ�һ���ރ�(n��i)ԓ�E�A�ϵ�һ�c(di��n)����
�ǵ�һ���ރ�(n��i)ԓ�E�A�ϵ�һ�c(di��n)����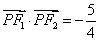 �����c(di��n)
�����c(di��n)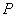 ������(bi��o)��
������(bi��o)��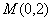 ��ֱ���c�E�A���ڲ�ͬ�ă��c(di��n)
��ֱ���c�E�A���ڲ�ͬ�ă��c(di��n)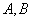 ����
���� ���J�ǣ�����O������(bi��o)ԭ�c(di��n)������ֱ��
���J�ǣ�����O������(bi��o)ԭ�c(di��n)������ֱ��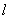 ��б��
��б��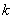 ��ȡֵ������
��ȡֵ�������鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
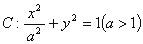 ������c(di��n)��
������c(di��n)�� ,���c(di��n)��
,���c(di��n)��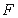 ,ֱ��
,ֱ�� �c�A
�c�A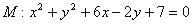 ����.�^(gu��)�c(di��n)
����.�^(gu��)�c(di��n)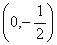 ��ֱ���c�E�A
��ֱ���c�E�A ����
���� ���c(di��n).
���c(di��n).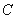 �ķ���;
�ķ���;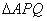 ����e�_(d��)�����r(sh��),��ֱ���ķ���.
����e�_(d��)�����r(sh��),��ֱ���ķ���.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
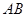 ���^(gu��)���タ
���^(gu��)���タ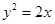 ���c(di��n)���ң�
���c(di��n)���ң�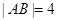 ���t
���t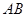 ���c(di��n)�ęM����(bi��o)��
���c(di��n)�ęM����(bi��o)�� �鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
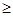
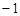 ��m
��m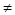 0)���c(di��n)P��܉�E����M��N���c(di��n)��(g��u)������C.
0)���c(di��n)P��܉�E����M��N���c(di��n)��(g��u)������C.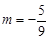 ������C�^(gu��)�c(di��n)Q (2��0) б�ʞ�
������C�^(gu��)�c(di��n)Q (2��0) б�ʞ�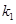 ��ֱ��
��ֱ��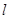 �c����C���ڲ�ͬ�ă��c(di��n)A�pB��AB���c(di��n)��R��ֱ��OR (O������(bi��o)ԭ�c(di��n))��б�ʞ�
�c����C���ڲ�ͬ�ă��c(di��n)A�pB��AB���c(di��n)��R��ֱ��OR (O������(bi��o)ԭ�c(di��n))��б�ʞ�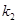 �����C
�����C 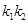 �鶨ֵ��
�鶨ֵ��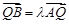 ����
����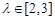 ����
����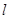 ��y�S�ϵĽؾ��׃������.
��y�S�ϵĽؾ��׃������.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
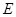 ��
��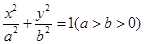 ���ҽ��c(di��n)
���ҽ��c(di��n)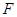 ���^(gu��)ԭ�c(di��n)��
���^(gu��)ԭ�c(di��n)��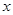 �S���غϵ�ֱ���c�E�A
�S���غϵ�ֱ���c�E�A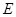 �ཻ��
�ཻ��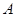 ��
��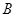 ���c(di��n)����
���c(di��n)����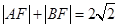 ��
��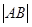 ��Сֵ��
��Сֵ��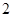 ��
�� �ķ��̣�
�ķ��̣�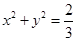 ���о�
���о�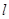 �c�E�A
�c�E�A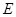 �ཻ��
�ཻ��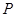 ��
��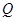 ���c(di��n)����(d��ng)
���c(di��n)����(d��ng)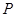 ��
��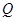 ���c(di��n)�M����(bi��o)����ȕr(sh��)����(w��n)��
���c(di��n)�M����(bi��o)����ȕr(sh��)����(w��n)��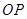 �c
�c �Ƿ�ֱ������ֱ��Ո(q��ng)�o���C����������ֱ��Ո(q��ng)�f(shu��)�����ɣ�
�Ƿ�ֱ������ֱ��Ո(q��ng)�o���C����������ֱ��Ո(q��ng)�f(shu��)�����ɣ��鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com