
已知二次函數f(x)=ax2+bx,f(x+1)為偶函數,函數f(x)的圖象與直線y=x相切.
(I)求f(x)的解析式;
(II)已知k的取值范圍為[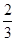 ,+∞),則是否存在區間[m,n](m<n),使得f(x)在區間[m,n]上的值域恰好為[km,kn]?若存在,請求出區間[m,n];若不存在,請說明理由.
,+∞),則是否存在區間[m,n](m<n),使得f(x)在區間[m,n]上的值域恰好為[km,kn]?若存在,請求出區間[m,n];若不存在,請說明理由.
解:(1)∵f(x+1)為偶函數,∴f(-x+1)=f(x+1),
即a(-x+1)2+b(-x+1)=a(x+1)2+b(x+1)恒成立,
即(2a+b)x=0恒成立,∴2a+b=0,∴b=-2a,∴f(x)=ax2-2ax,
∵函數f(x)的圖象與直線y=x相切,
∴二次方程ax2-(2a+1)x=0有兩相等實數根,∴Δ=(2a+1)2-4a×0=0,
∴a=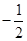 ,f(x)=-
,f(x)=-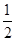 x2+x.
......5分
x2+x.
......5分
(2)∵f(x)=-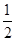 (x-1)2+
(x-1)2+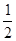 ≤
≤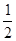 ,
,
∴[km,kn]⊆(-∞,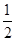 ],∴kn≤
],∴kn≤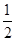 ,又k≥
,又k≥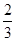 ,∴n≤
,∴n≤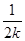 ≤
≤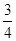 ,
,
又[m,n]⊆ (-∞,1],f(x)在[m,n]上是單調增函數,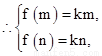 即-
即-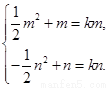
即m,n為方程-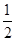 x2+x=kx的兩根,解得x1=0,x2=2-2k. ∵m<n且k≥
x2+x=kx的兩根,解得x1=0,x2=2-2k. ∵m<n且k≥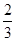 .
.
故當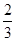 ≤k<1時,[m,n]=[0,2-2k];
當k>1時,[m,n]=[2-2k,0]; 當k=1時,[m,n]不存在.
≤k<1時,[m,n]=[0,2-2k];
當k>1時,[m,n]=[2-2k,0]; 當k=1時,[m,n]不存在.
【解析】略


科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 3 |
| x |
| 1 |
| 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| bx-1 | a2x+2b |
查看答案和解析>>
科目:高中數學 來源: 題型:
| bx-1 | a2x+2b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com