
(本小題滿分15分)(文)如圖,在四棱錐P-ABCD中,底面為直角梯形,AD//BC,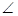 BAD=
BAD=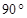 ,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分別為PC、PB的中點(diǎn).
,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分別為PC、PB的中點(diǎn).

(Ⅰ)求證:PB⊥DM;
(Ⅱ) 求CD與平面ADMN所成角的余弦
解:方法一:
(Ⅰ)因?yàn)镹是PB的中點(diǎn),PA=AB,
所以AN⊥PB。
因?yàn)锳D⊥平面PAB,所以AD⊥PB,
從而PB⊥平面ADMN,
因?yàn)镈M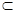 平面ADMN,
平面ADMN,
所以PB⊥DM。
(Ⅱ)取AD的中點(diǎn)G,連結(jié)BG、NG,
則BG//CD,
所以BG與平面ADMN所成的角和CD與平面ADMN
所成的角相等。
因?yàn)镻B⊥平面ADMN,
所以∠BGN是BG與平面ADMN所成的角。
在Rt△BGN中,
sin∠BGN=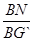 =
=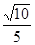 。
。
故CD與平面ADMN所成的角是arcsin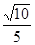 。
。
方法二:
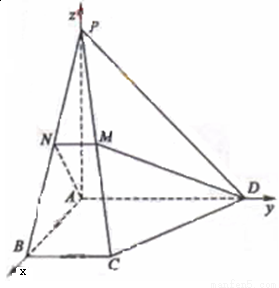
如圖,以A為坐標(biāo)原點(diǎn)建立空間直角坐標(biāo)系A(chǔ)-xyz,設(shè)BC=1,則
A(0,0,0),P(0,0,2),B(2,0,0),C(2,1,0),M(1,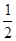 ,1),D(0,2,0)。
,1),D(0,2,0)。
(Ⅰ) 因?yàn)?/p>
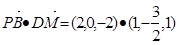
=0,所以PB⊥DM。
(Ⅱ) 因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052600431027731733/SYS201205260044501365955881_DA.files/image007.png"> =0,
所以PB⊥AD,
又因?yàn)镻B⊥DM,
所以PB⊥平面ADMN。
因此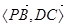 的余角即是CD與平面ADMN所成的角
的余角即是CD與平面ADMN所成的角
因?yàn)?/p>
 =
=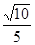 ,
,
所以CD與平面ADMN所成的角為arcsin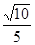 .
.
【解析】略


 開心蛙狀元作業(yè)系列答案
開心蛙狀元作業(yè)系列答案 課時(shí)掌控隨堂練習(xí)系列答案
課時(shí)掌控隨堂練習(xí)系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學(xué)業(yè)水平測(cè)試系列答案
浙江之星學(xué)業(yè)水平測(cè)試系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年福建省高三上學(xué)期期中理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分15分)
已知函數(shù)
(Ⅰ)求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若 ,試分別解答以下兩小題.
,試分別解答以下兩小題.
(ⅰ)若不等式 對(duì)任意的
對(duì)任意的 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù) 的取值范圍;
的取值范圍;
(ⅱ)若 是兩個(gè)不相等的正數(shù),且
是兩個(gè)不相等的正數(shù),且 ,求證:
,求證: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年浙江省高三下學(xué)期3月聯(lián)考理科數(shù)學(xué) 題型:解答題
(本小題滿分15分).
已知 、
、 分別為橢圓
分別為橢圓 :
: 的
的
上、下焦點(diǎn),其中 也是拋物線
也是拋物線 :
: 的焦點(diǎn),
的焦點(diǎn),
點(diǎn) 是
是 與
與 在第二象限的交點(diǎn),且
在第二象限的交點(diǎn),且 。
。
(Ⅰ)求橢圓的方程;
(Ⅱ)已知點(diǎn)P(1,3)和圓 :
: ,過點(diǎn)P的動(dòng)直線
,過點(diǎn)P的動(dòng)直線 與圓
與圓 相交于不同的兩點(diǎn)A,B,在線段AB取一點(diǎn)Q,滿足:
相交于不同的兩點(diǎn)A,B,在線段AB取一點(diǎn)Q,滿足: ,
, (
( 且
且 )。求證:點(diǎn)Q總在某定直線上。
)。求證:點(diǎn)Q總在某定直線上。

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年浙江省高三上學(xué)期第三次月考數(shù)學(xué)文卷 題型:解答題
(本小題滿分15分)
如圖已知,橢圓 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為 、
、 ,過
,過 的直線
的直線 與橢圓相交于A、B兩點(diǎn)。
與橢圓相交于A、B兩點(diǎn)。
(Ⅰ)若 ,且
,且 ,求橢圓的離心率;
,求橢圓的離心率;
(Ⅱ)若 求
求 的最大值和最小值。
的最大值和最小值。

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆浙江省寧波市高一上學(xué)期期末考試數(shù)學(xué) 題型:解答題
(本小題滿分15分)若函數(shù) 在定義域內(nèi)存在區(qū)間
在定義域內(nèi)存在區(qū)間 ,滿足
,滿足 在
在 上的值域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052202033078124869/SYS201205220205036875888611_ST.files/image002.png">,則稱這樣的函數(shù)
上的值域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052202033078124869/SYS201205220205036875888611_ST.files/image002.png">,則稱這樣的函數(shù) 為“優(yōu)美函數(shù)”.
為“優(yōu)美函數(shù)”.
(Ⅰ)判斷函數(shù) 是否為“優(yōu)美函數(shù)”?若是,求出
是否為“優(yōu)美函數(shù)”?若是,求出 ;若不是,說明理由;
;若不是,說明理由;
(Ⅱ)若函數(shù) 為“優(yōu)美函數(shù)”,求實(shí)數(shù)
為“優(yōu)美函數(shù)”,求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011年江蘇省高二下學(xué)期期中考試?yán)頂?shù) 題型:解答題
(本小題滿分15分)在5道題中有3道理科題和2道文科題,如果不放回地依次抽取2道題.求:
(1)第1次抽到理科題的概率;
(2)第1次和第2次都抽到理科題的概率;
(3)在第1次抽到理科題的條件下,第2次抽到文科題的概率
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com