
��ֱ֪��l��(j��ng)�^�c(di��n)(0����2)����Aб����60�㣮
(1)��ֱ��l�ķ��̣�
(2)��ֱ��l�c������(bi��o)�S���������ε���e��
(1) 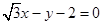 (2)
(2)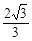
����ԇ�}������(1)��?y��n)�ֱ��l�ăAб�ǵĴ�С��60��,����б�ʞ�tan 60�㣽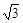 ����ֱ��l��(j��ng)�^�c(di��n)
����ֱ��l��(j��ng)�^�c(di��n)
(0����2)�������䷽�̞�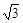 x��y��2��0��
x��y��2��0��
(2)��ֱ��l�ķ���֪����x�S��y�S�ϵĽؾ�քe�� ����2������ֱ��l�c������(bi��o)�S���������ε���eS��
����2������ֱ��l�c������(bi��o)�S���������ε���eS�� ��
�� ��2��
��2��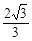
���c(di��n)��ֱ������
�c(di��n)�u��ֱ��������(bi��o)�S�ϵĽؾ��c���x�Dz�ͬ�ģ�����y�S�ϵĽؾ����cy�S���c(di��n)�Ŀv����(bi��o)���ؾ�Ľ^��ֵ���ڵ�ԭ�c(di��n)�ľ��x



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪ƽ���(n��i)һ���c(di��n) ���c(di��n)
���c(di��n)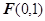 �ľ��x�c�c(di��n)
�ľ��x�c�c(di��n) ��
�� �S�ľ��x�IJ����1����I������c(di��n)
�S�ľ��x�IJ����1����I������c(di��n) ��܉�E
��܉�E �ķ��̣���II���^�c(di��n)
�ķ��̣���II���^�c(di��n) ���ɗlб�ʴ����һ��ഹֱ��ֱ��
���ɗlб�ʴ����һ��ഹֱ��ֱ�� ���O(sh��)
���O(sh��)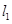 �c܉�E
�c܉�E �ཻ���c(di��n)
�ཻ���c(di��n) ��
�� �c܉�E
�c܉�E �ཻ���c(di��n)
�ཻ���c(di��n) ����
���� ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ �У��c(di��n)
���c(di��n)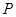 �����c(di��n)
�����c(di��n)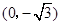 ��
�� �ľ��x֮�͵���4���O(sh��)�c(di��n)
�ľ��x֮�͵���4���O(sh��)�c(di��n)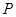 ��܉�E��
��܉�E��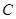 ��
��
������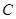 �ķ��̣�
�ķ��̣�
�����O(sh��)ֱ�� �c
�c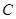 ����
����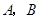 ���c(di��n)��k���ֵ�r
���c(di��n)��k���ֵ�r
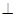
 ���˕r
���˕r ��ֵ�Ƕ��٣�
��ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)�E�A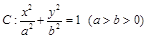 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe�� ������c(di��n)��
������c(di��n)�� ���x���ʞ�
���x���ʞ� �� ��
�� ��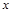 �Sؓ(f��)���S����һ�c(di��n)
�Sؓ(f��)���S����һ�c(di��n) ����
����
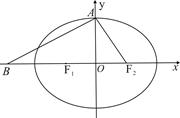
��1�����^ ���c(di��n)�ĈA ǡ���cֱ��
���c(di��n)�ĈA ǡ���cֱ��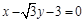 ���У���E�AC�ķ��̣�
���У���E�AC�ķ��̣�
��2���ڣ�1���ėl���£��^�ҽ��c(di��n) ��б�ʞ�
��б�ʞ�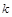 ��ֱ��
��ֱ�� �c�E�AC����
�c�E�AC���� ���c(di��n)����
���c(di��n)����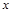 �S���Ƿ�����c(di��n)
�S���Ƿ�����c(di��n)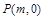 ��ʹ����
��ʹ����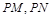 ����߅��ƽ����߅�������Σ�������ڣ����
����߅��ƽ����߅�������Σ�������ڣ���� ��ȡֵ��������������ڣ��f�����ɣ�
��ȡֵ��������������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ֱ֪��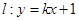 �^���c(di��n)
�^���c(di��n) �����c(di��n)
�����c(di��n) �M��
�M��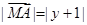 �����c(di��n)
�����c(di��n) ��܉�E��
��܉�E�� .
.
������ �ķ��̣�
�ķ��̣�
����ֱ��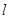 �c
�c ����
����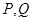 ���c(di��n)����
���c(di��n)����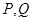 �����c(di��n)�քe��
�����c(di��n)�քe�� ���о������о������c(di��n)
�������������c(di��n) .
.
�����C��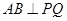 ������ֱ��
������ֱ�� �c
�c ����
����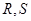 ���c(di��n)������߅��
���c(di��n)������߅��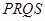 ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪������ԭ�c(di��n)�����c(di��n)������(bi��o)�S�ϵęE�A �������x���ʞ�
�������x���ʞ�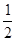 ��һ�����c(di��n)�͒��タ
��һ�����c(di��n)�͒��タ �Ľ��c(di��n)�غ�,�^ֱ��
�Ľ��c(di��n)�غ�,�^ֱ�� ��һ�c(di��n)
��һ�c(di��n)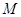 ���E�A
���E�A �ăɗl�о������c(di��n)�քe��
�ăɗl�о������c(di��n)�քe��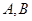 .
.
������E�A �ķ��̣�
�ķ��̣�
�������ڙE�A �ϵ��c(di��n)
�ϵ��c(di��n) ̎�ęE�A���о�������
̎�ęE�A���о������� . ���C:ֱ��
. ���C:ֱ�� ���^���c(di��n)
���^���c(di��n)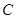 ���������c(di��n)
���������c(di��n)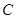 ������(bi��o).
������(bi��o).
�����Ƿ���ڌ�(sh��)��(sh��) ��ʹ��
��ʹ�� �������(�c(di��n)
�������(�c(di��n)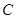 ��ֱ��
��ֱ�� ���^�Ķ��c(di��n))�����ڣ����
���^�Ķ��c(di��n))�����ڣ���� ��ֵ���������ڣ�Ո�f�����ɡ�
��ֵ���������ڣ�Ո�f�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�p���� ���x����
���x����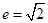 ���c(di��n)
���c(di��n)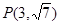 ���p����C��.
���p����C��.
(1)���p����C�ķ��̣�
(2)ӛO������(bi��o)ԭ�c(di��n)���^�c(di��n)Q (0,2)��ֱ��l�c�p����C�ཻ�ڲ�ͬ�ă��c(di��n)E��F������OEF����e�� ��ֱ��l�ķ���.
��ֱ��l�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D���O(sh��)���タ ��
�� ���Ĝ�(zh��n)���c
���Ĝ�(zh��n)���c �S����
�S���� �����c(di��n)��
�����c(di��n)�� ����
���� ��
�� �齹�c(di��n)���x����
�齹�c(di��n)���x���� �ęE�A
�ęE�A �c���タ
�c���タ ��
�� �S�Ϸ���һ�����c(di��n)��
�S�Ϸ���һ�����c(di��n)��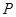 .
.
��1����(d��ng)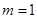 �r����E�A�ķ��̣�
�r����E�A�ķ��̣�
��2���ڣ�1���ėl���£�ֱ�� ��(j��ng)�^�E�A
��(j��ng)�^�E�A ���ҽ��c(di��n)
���ҽ��c(di��n) ���c���タ
���c���タ ����
���� ��
��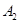 ������Ծ���
������Ծ��� ��ֱ�����A��ԇ�Д��c(di��n)
��ֱ�����A��ԇ�Д��c(di��n)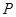 �c�A��λ���P(gu��n)ϵ�����f�����ɣ�
�c�A��λ���P(gu��n)ϵ�����f�����ɣ�
��3���Ƿ���ڌ�(sh��)��(sh��) ��ʹ��
��ʹ�� ��߅�L���B�m(x��)����Ȼ��(sh��)�������ڣ�����@�ӵČ�(sh��)��(sh��)
��߅�L���B�m(x��)����Ȼ��(sh��)�������ڣ�����@�ӵČ�(sh��)��(sh��) ���������ڣ�Ո�f�����ɣ�
���������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����С�}�M��12�֣�
��֪�E�A������ԭ�c(di��n)�����c(di��n)��y�S�ϣ�������4���x���ʞ� ��
��
��I����E�A���̣�
��II���O(sh��)�E�A��y�S�������S�ϵĽ��c(di��n)��M�����c(di��n)A���c(di��n)B�ڙE�A�ϣ���M������ ���ɵıȞ�2����AB����ֱ���ķ��̣�
���ɵıȞ�2����AB����ֱ���ķ��̣�
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com