
 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源:不詳 題型:解答題
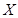 ,求
,求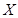 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 的概率分布如下表,且
的概率分布如下表,且 ,則
,則 的值為( )
的值為( ) |  |  |  |  | ||||
 |  |  |  | 
查看答案和解析>> 同步練習冊答案 湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。 ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號 |